PHYS 252

Prologue

For this assignment, you will need four formulas describing the Keplerian orbit of a test particle around the Sun:

1. Its radius r versus angle θ is given by the ellipse:
   
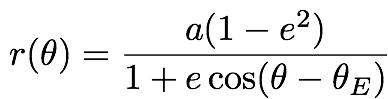   where a is the semimajor axis, e is the eccentricity, and θ_E is the orientation of the ellipse; specifically, it gives the angle of closest approach to the Sun ("periapse").
2. Its energy per unit mass is
   
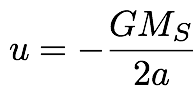
   where M_S is the Sun's mass.
3. Its angular momentum per unit mass is
   
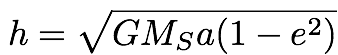
4. Its orbital period is
   
   

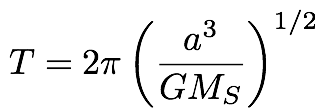
Note that energy and angular momentum per unit mass are defined as


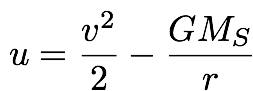
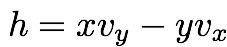
where v_x and v_y are the Cartesian components of the velocity, v = ( v_x² + v_y²)^1/2, and x = r cos(θ), and y = r sin(θ)

Assignment #9
[10 pts due 2pm, May 3]

1. Write a code integrating the equations of motion for a test particle orbiting the Sun.
   
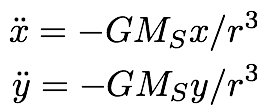
   Use 4th-order Runge-Kutta. You should measure time in units of years, and length in units of AU; so, what should you set GM_S equal to? Initialize a particle (Earth) at x=1, y=0, v_x=0, v_y=2π, and integrate.
   • Plot its x vs. y. To make the x vs. y plot look like a circle in gnuplot, first type "set size square", and then something like "plot [-1.5:1.5] [-1.5:1.5] 'out.dat' ".
   • What is the orbital period, and what should it be?
   • Repeat simulation, but initialized with v_x=1 and v_y=2π+1. Plot its x vs y on the same graph as before.
2. Write two functions to transform between the Cartesian variables used in your integrator and the particle's position relative to an ellipse. One of the functions, "ellipse_to_xy", will take as input the four quantities a, e, θ, and θ_E, and output the four quantities x, v_x, y, v_y. The second function, "xy_to_ellipse" will do the opposite. To test (and show me) that your code works, choose 4 random numbers for a, e, θ, and θ_E (.1,.2,.4,.3), apply ellipse_to_xy and print out x,vx,y,vy. Then apply xy_to_ellipse to recover the original values.
   
   Note: it is straightforward algebra to use formulas i-iii above (together with the definitions of u and h) to derive the transformation laws. A few hints:
   • In "ellipse_to_xy", to calculate v_x and v_y, you can define α such that v_x=v cosα and v_y=v sinα. Then one can write h=xv_y-yv_x= rv sin(α-θ), and use that to solve for α.
   • In "xy_to_ellipse", to get θ, check out the function atan2 in "math.h"
   • In "xy_to_ellipse", getting θ_E can be a little tricky. (And you will need it below.) There are two things to note. If you use formula i above, you will need to do an "acos" (inverse cosine). But this always returns an angle between 0 and π . To account for when θ -θ_E lies between -π and 0, you will need an if statement: check if the radial velocity v_r= (x v_x + y v_y)/v is positive, i.e. if the particle is going from its periapse (point of closest approach) to apoapse (point of furthest distance). If so, then θ -θ_E should lie between 0 and π and you're done. If not, flip the sign of θ -θ_E. The second tricky thing is that your expression for θ_E will likely blow up when e=0. I will let you figure out how to handle this.
3. Using your functions from question 2, initialize a test particle ("Mercury") with a=0.39AU and e=0.206, θ_E = -3π/4 and its initial angle θ = θ_E. Integrate, and plot y vs. x and r vs. θ , as output from your simulation. Also superimpose on these plots the analytic formula for an ellipse (formula i in Prologue above). Make sure you (and I) can see that the theory matches the simulation.
4. Calculate the effect of Jupiter on the precession of Mercury's perihelion. Do not bother integrating Jupiter's equation of motion. Just force Jupiter to have a circular orbit, with radius equal to its semimajor axis. Start Mercury as in question 3. Use the function "xy_to_ellipse" to output Mercury's θ_E as a function of time, and hand in the plot. From that, what is the rate at which Jupiter causes Mercury's perihelion to precess? Quote your answer both in radians per year, and in arcseconds per century, and estimate the error in your precession rate.
5. [BONUS QUESTION] Repeat question 4, but now include the planets Venus, Earth, Mars, Jupiter, and Saturn (Uranus and Neptune are unimportant.). Treat all of those planets as you did Jupiter. What is your result for the precession rate, and with what error? How does this compare with the pre-general-relativity result of 531 arcseconds per century? (When I did this question, I got a slightly different answer. The observed result is 574 arcseconds per century. )
6. [BONUS QUESTION]
   1. Reproduce Figure 4.15 (both panels). You can force Jupiter to have a circular orbit.
   2. The energy of the test particle is conserved in the rotating frame of Jupiter. The energy in the rotating frame (per unit mass) is:
      
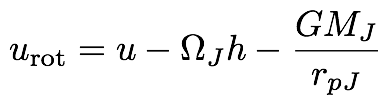      where Ω_J is Jupiter's angular speed, and r_pJ is the distance of the test particle (or asteroid) from Jupiter. You should first check for yourself that u_rot is conserved. Now, choose u_rot equal to its value for the orbit in the left-hand panel of Figure 4.15. Select a range of orbits with the same value of u_rot. And plot a Poincaré section of these orbits. For this Poincaré section, plot the asteroid's radial velocity versus its radial position every time the asteroid has the same angular position as Jupiter.