Conservation Laws
Over the years, physicists have gradually discovered that there are many aspects of the physical world which are conserved, i.e., their sum totals never change. Here are the conservation laws we know about:
Conservation Of Mass -- This law is easy to understand if you think of the world as being made up only of indestructible, impenetrable particles such as protons, neutrons, and electrons. (This is not correct, in fact, because even elementary particles can be destroyed in high-energy reactions....but for now, and as a convenient way to think about conservation of mass, the indestructible particle picture is good enough.) The particles can be moved around, but their number is conserved.
Conservation Of Electric Charge -- Protons have a plus charge (call it +1), and electrons have a negative charge (call it -1), and the total sum of all the plusses and minuses in the Universe never changes. This law always holds true, even in the most exotic subatomic reactions. As far as we can tell, the total charge of the Universe is exactly zero.
Conservation Of Nuclear Properties -- We will deal with these laws later in the course. Suffice to say that subatomic particles have numerous "numbers" associated with them whose sums, like that of electric charge, never change.
Conservation Of Energy -- As discussed in the previous section, energy can assume many different guises, but the sum total of all the different guises is constant.
Conservation Of Linear Momentum -- This is more-or-less a different way of phrasing Newton's law of action-reaction. Suppose I throw a baseball in one direction. Then there must be an equal and opposite reaction in the other direction. We say that the baseball and the person throwing the baseball have acquired equal amounts of momentum, but pointed in opposite directions.
To be precise, the momentum p is defined as p = Ft. In other words, momentum is caused by a force acting over time. (Not to be confused with WORK, or E = Fd, which is a force acting through a distance.) The definition of momentum means that:
Since velocity has a direction, momentum also has a direction. This directional dependence means that the momentum along each spatial axis (imagine space to have three axes, labeled x, y, and z as on 3D graph paper) is conserved separately.
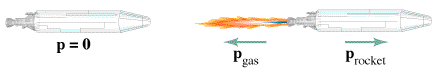
Above, an object with zero momentum gains a positive momentum p while the fuel gains an equal and opposite momentum. Click here for a Quicktime movie of two objects with equal and opposite momentum combining to form one object with zero momentum. (No country singers were harmed in the making of this clip.)
Conservation Of Angular Momentum -- This is more or less the action-reaction law restated for rotational motion. If I try to rotate anything in a clockwise direction, then there will be a reaction force in the counter-clockwise direction. Angular momentum, like linear momentum, has a direction associated with it -- but it's probably not the direction you think. For angular momentum, the direction lies along the axis of rotation, not with or against the rotation. Just as an object in linear motion has inertia, and cannot be changed in direction without a force acting on it, so the direction of the axis of a rotating object has a rotational inertia which cannot be changed without a force acting on it.
 Conservation of angular momentum is why a spinning top (or more technically, a gyroscope) will not fall over even when it is leaning at an angle on a support post. (See cartoon at left.) The angular momentum present in the wheels of a bicycle is what makes a moving bicycle so stable, because the axis of rotation of the wheels is parallel to the ground and it strongly resists being tipped over. A bicycle that is not moving has no such angular momentum, and therefore is quite tricky to keep balanced.
Conservation of angular momentum is why a spinning top (or more technically, a gyroscope) will not fall over even when it is leaning at an angle on a support post. (See cartoon at left.) The angular momentum present in the wheels of a bicycle is what makes a moving bicycle so stable, because the axis of rotation of the wheels is parallel to the ground and it strongly resists being tipped over. A bicycle that is not moving has no such angular momentum, and therefore is quite tricky to keep balanced.
Changing the diameter of a rotating object demonstrates another aspect of the conservation of angular momentum. We still have p = mv, but v for a point on a rotating object is dependent on both the radius of rotation and the rate of rotation. If I move the point inward (decreasing radius) then the rotation rate must increase to compensate. This effect is what causes a spinning ice skater to spin faster and faster as she pulls in her arms.
 Energy page
|
Atoms and Heat
Energy page
|
Atoms and Heat 