Electricity & Magnetism
The interactions of electricity and magnetism are difficult to explain in nontechnical terms. This is primarily because one has to describe the interactions in terms of invisible "force fields" which shift, expand, contract, strengthen, weaken, and rotate in space, and these are very difficult to describe adequately in verbal terms. In mathematical terms, coupled sets of three-dimensional vector differential equations are required, and these are also quite difficult to visualize.
So, we will go light on the mathematics as we discuss E & M. We will rely on more intuitive, graphical interpretations. Here are the basics:
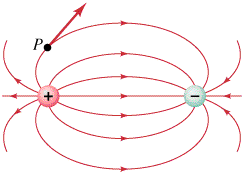 Electric field for two equal but opposite charges. The electric force at any point P is tangent to the electric field. 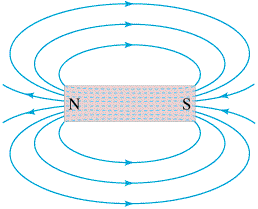 Magnetic field around a bar magnet. Note the close similarity to the electric field in the previous illustration. |
The electrostatic force between two point charges is given by Coulomb's Law:
where: k = the electrostatic constant = 8.99 X 109 kg m3 / s2 coul2, r = the distance between the two charges, and q1 and q2 are the two charges, measured in coulombs. (One coulomb = the charge on 6.24 X 1018 electrons. Therefore, one proton or electron carries a charge of ±1.602 X 10-19 coulomb.) If q1 and q2 have the same sign, the electrostatic force is repulsive. If they have opposite signs, the force is attractive. Notice how the formula for electrostatic force looks exactly like that for gravity: all we have to do is substitute the gravitational constant G for the electrostatic constant k, and switch mass for charge.
2) Static magnetic fields are not described by a simple formula, because magnets always have a north pole and a south pole, so the magnetic field always loops from one pole to the other. If one immerses a magnet in a heavy fluid which contains iron filings, and shakes the container, the iron filings will align themselves along the magnetic field and thus reveal the shape of the field. The field shown at right is the simplest possible magnetic field. Both this and the field shown in the previous illustration are called dipole fields, because they are created by two poles.
Although there is no simple formula for magnetostatic force, there is a magnetic force constant "m" which is analogous to "k" for electric fields and to "G" for gravity. m is equal to 1.26 X 10-6 in metric units.
3) Electricity and magnetism are essentially two aspects of the same thing, because a changing electric field creates a magnetic field, and a changing magnetic field creates an electric field. (This is why physicists usually refer to "electromagnetism" or "electromagnetic" forces together, rather than separately.)
To demonstrate that an electric current (i.e., moving electric charge) generates a magnetic field, all you need do is simply place a magnetic compass next to a wire in a circuit. When current is passed through the wire, the compass will deflect, indicating the presence of a magnetic field circling the wire. (In fact, this is exactly how the magnetic field of a current was discovered. In 1819, Professor Hans Oersted of the University of Copenhagen was giving a lecture on electric currents and also on magnets. He happened to leave a compass next to a conducting wire, and in the middle of the lecture he noticed that the current was deflecting the compass. This is probably the only important physics discovery ever made before a live audience.) It is important to understand that the Coulomb force law only provides the full story of the forces between two charges when the charges are standing still. (That's why it's referred to as an electrostatic force law.) The forces between moving electric charges are much more complicated, and in fact, what we call a "magnetic field" is actually just the result of moving charges acting on each other. Static magnetic fields in materials such as iron are more-or-less caused by the motion of electrons within atoms.
One can also use a magnet and some loops of wire to demonstrate the reverse of the above: that a changing magnetic field creates a current. (This is called induction.) By simply moving a magnet through a coil of wire, one can easily detect the current flowing in the coil by using a sensitive ammeter. But if the magnet is held still inside the loop, nothing will happen. Only a changing (read: moving, expanding, oscillating, rotating) magnetic field gives rise to electric currents. Likewise, only moving charges (currents) give rise to magnetic fields. Unmoving charges produce only the Coulomb force.
The simple demonstrations outlined above are very similar to their industrial counterparts. A commercial electric generator is little more than a coil of wire which is rotated inside a circular arrangement of magnets. And an electric motor is little more than a current-carrying coil whose magnetic field is interacting with the field of a circular arrangement of magnets. In other words, the only difference between a generator and a motor is whether you put in force to get out current, or put in current to get out force. The two types of devices are completely symmetric. If you turn the blade on an electric fan with your finger, then you have made it into an electric generator. I often demonstrate this fact in class with hand-held electric generators. By turning the crank on one generator, I can send enough current through a small lightbulb to make it light up. This proves it is a generator. But by connecting two identical generators to each other, I can also show that cranking the handle on one generator makes the handle on the other generator turn by itself, thus proving that the second generator is now acting as a motor.
So much for E & M per se.
In 1864 the Scottish physicist James Clerk Maxwell derived a set of equations for electromagnetism which we today call Maxwell's equations. (He developed many other important equations besides these, but never mind. When physicists refer to Maxwell's equations, these are the ones they mean.)
While he was working on these equations, it occurred to Maxwell that if one could...in some way...produce a disembodied magnetic field in space, and set it to oscillating, then it would produce an electric field. (Similar to the way an oscillating magnetic field can induce an electric current.) Then, the oscillating electric field would produce a magnetic field. And so on, in an endless cycle. Maxwell was able to show that, if such a thing were to be created, the electric and magnetic fields would oscillate at right angles to each other (one wave going up and down, the other going in and out) and would travel together while shifting their energy back-and-forth as they constantly and dynamically regenerated each other. In other words, you would have electric and magnetic fields existing by themselves, with no charges, no magnets, and no masses. Maxwell calculated that the speed of this wave would be:
where k and m are the electric and magnetic force constants. If we insert the values given earlier, we have: (4 X 3.14159 X 8.99 X 109 / 1.26 X 10-6)½ = 2.99 X 108 m/s. Which is the speed of light. Although this did not prove that light was the mutually perpendicular electric and magnetic wave couplet which Maxwell envisioned, it was certainly suggestive, and Maxwell did suggest that light was an electromagnetic wave. Maxwell's picture of a light wave is illustrated below.
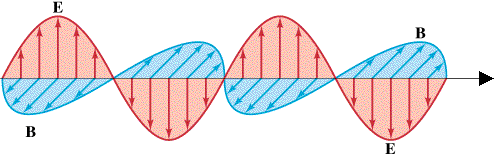Maxwell died rather young, at the age of 48, and it was left to others to extend his work. Throughout the 1870's and 1880's his equations were applied to a number of problems in electromagnetism (mostly by British physicists, because Maxwell's work did not really catch on outside the British Isles until 1888). It gradually became clear to a number of people that Maxwell's equations predicted that electromagnetic waves should always be produced any time you had electric charges under acceleration. In rough terms, accelerating charges always "shed" electromagnetic waves more-or-less like a speedboat sheds water waves.Did this mean that ordinary electric circuits were giving off invisible waves as the electricity moved around? According to Maxwell, it seemed that they ought to be.
To make a long story short, a few people did begin looking for invisible waves, and in 1888 the German physicist Heinrich Hertz (one of the few German physicists who thought maybe Maxwell had something here) discovered radio waves. This created quite a sensation, and from that point onward Maxwell's theory of electromagnetism was established as the best one.
This property of moving charges is why the airlines usually request that you turn off stereos and so forth during takeoffs and landings. If it uses electricity, then it produces radio noise at some level, and that is that. This can interfere with air navigation. I sometimes overhear fellow passengers grumbling that it's silly, their portable CD player isn't a radio so what's the problem....but that only proves that their knowledge of radio waves is 114 years out of date. You can't stop accelerating electric charges from producing E & M waves any more than you can dive into a swimming pool without disturbing the water.
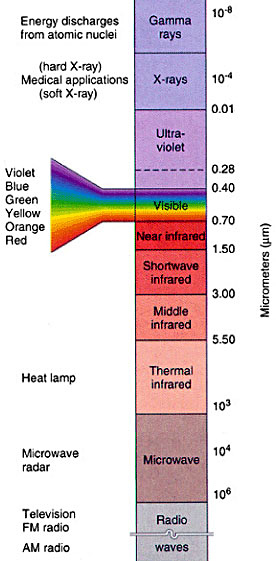
Electromagnetic waves form an entire spectrum, as seen in the figure at right. Radio waves, microwaves, light, x-rays, and all the other E & M waves are exactly the same
Back to our story. Not withstanding the many successes of Maxwell's theory, it was nonetheless clear to the physics world of 1894 that something was still terribly wrong with their understanding of E & M. The search for the ether...that near-magical fluid which the E & M waves were supposed to be waving within...was still going on, and most of the results didn't make any sense at all.
Probably the most puzzling result was the now-famous Michelson-Morley experiment of 1887. Albert Michelson and Edward Morley were professors at Case Western University in Cleveland, and they wanted to detect the motion of the Earth through the ether by looking at the speed of light as it moves in different directions. As the Earth zips through space in its orbit, one might expect that the speed of the light waves (relative to Earth) would be speeded up or slowed down, depending on whether the light is moving in the same direction as the Earth, or at 90° to the Earth's motion, etc. Michelson and Morley hoped to measure subtle differences in light interference patterns which would allow them to tell if the universal ether was standing still or flowing in some way.
Alas, to their immense puzzlement, they couldn't detect any differences in the speed of light at all!! Whether the Earth was moving in the same direction as the light in their experiment, or opposite to it, or at right angles to it, the result was always the same: the speed of light that they measured never varied. Since this is roughly equivalent to saying that the relative velocity between a train and a train station doesn't depend on whether the train is moving or not, Michelson and Morley were completely baffled. They worked on their experiment for years, improving it constantly and trying every variation they could think of, but they finally had to (reluctantly) conclude that they could not measure any difference in the speed of light regardless of its direction relative to the Earth, even though their equipment was at least 100 times more sensitive than necessary, if the ether theories were correct.
(Albert Michelson won the Nobel Prize in Physics in 1907, based in large part on his work on not measuring anything in 1887. The Michelson-Morley experiment is generally considered to be the most important null experiment in scientific history.)
Another experiment (not as famous as Michelson-Morley, but a personal favorite of mine) that didn't make much sense was the measurement of the speed of light through flowing water. The speed of light through any transparent material is given by c / n, where c = speed of light in a vacuum = 2.99 X 108 m/s, and n is the (dimensionless) index of refraction of the material. But technically, c / n is the speed of light in a material if the material is standing still. Some people wondered, if light is being transmitted by an ether, what speed would you measure if the water was flowing? One could easily imagine two cases:
1) The water does not interact with the ether at all, so the speed of light in water is unaffected and still equals c / n .
2) The water traps the ether and carries it along. In this case, the speed of light must be c / n + v, where v is the velocity of the water. i.e., lightspeed through the ether in the water = c / n , but the water is carrying the ether at v, so the resultant is just the two velocities added together.
The experiment was performed by Jean Foucault in 1850, and the result was:
Hmn. Great. The experiment didn't agree with either theory of ether interaction. The factor of (1 - 1/n2) was a puzzler. If you took it literally, it meant that the ether was neither standing still nor moving with the water, but partially "slipping" past it in some way. But how? Why? And what on Earth did the inverse square of the index of refraction have to do with anything? No one had a decent explanation for this experiment.
Around the turn of the century, an obscure filing clerk in the Swiss Patent Office began thinking about the problems with E & M, and what he thought about it will occupy our attention next.
Static Electricity
|
Relativity 
Ideas of Physics HomepageTranslation of this page to other languages: Estonian, French, Spanish, Ukrainian