
Johannes Kepler (1571 - 1630)
Johannes Kepler was born prematurely on December 27, 1571, in Weil, Swabia, a wine region in southwest Germany not far from France. As a seven-month child, Kepler was sickly from birth, and he contacted smallpox when very young. His vision was severely defective, and he had various other illnesses fairly constantly. He took twice as long as normal children to get through elementary Latin. This made it necessary for him to have a religious education, for he seemed fit for no post more strenuous than that of a minister. Kepler went to the University of Tubingen, a Protestant institution, where he studied mainly theology and philosophy, but also mathematics and astronomy. (The Dukes of Wurtenberg, after becoming Lutheran, had put an efficient educational system in place, with grants and scholarships for the poor, to ensure that the universities could produce a supply of well-educated clergymen capable of defending the new faith in the religious controversies raging at the time.)At the university, Kepler's exceptional intellectual abilities became apparent. He greatly admired the astronomy professor Maestlin, who publicly taught the Ptolemaic scheme, but privately believed Copernicus. Kepler himself defended Copernicus' scheme in a public debate. Unfortunately for him, this ensured he would not be offered a faculty position at Tubingen when he graduated. (Luther himself had mocked Copernicus' scheme, and quoted scripture to prove it wrong.) Instead, Kepler was offered a professorship of astronomy in faraway Graz, Styria (now part of Austria), where he went in 1594.
While at Graz, Kepler (already a confirmed Copernican) began to wonder, why did the Creator make the orbits of the planets the particular sizes they are? He felt the Universe should somehow show mathematical beauty or symmetry. Arguing in a way that Pythagoras and Plato would have sympathized with, he suggested that the orbits might be arranged so that regular polygons (triangles, squares, etc.) would just fit between adjacent ones, and maybe somehow this reflected an invisible underlying structure holding it all together. Thinking in three dimensions, he created a model in which concentric spheres had a regular solid, such as a tetrahedron, placed between them such that the outer sphere would touch the vertices of the solid, and the inner sphere would touch all its sides. The really exciting part -- in Kepler's view -- is that there were just six planets, which means five spaces between the spheres, and there are just five regular solids! Thus, if the distances came out right, the theory provided a complete explanation, in terms of an elegant geometric model, of why there are just six planets, and why they are spaced as we find them.
 Actually, the distances don't come out right, especially for Jupiter, but Kepler was so sure of the rightness of his scheme that he blamed the discrepancies on errors in Copernicus' tables! He modestly entitled his work "Mysterium Cosmographicum -- The Mystery of the Universe Explained". (Sounds like the New Age fog they carry at Borders, doesn't it? The two aren't much different.) The crucial illustration from his book is shown at left. The outer sphere represents the orbit of Saturn, and the central part (representing the inner solar system) is shown magnified at top right.
Actually, the distances don't come out right, especially for Jupiter, but Kepler was so sure of the rightness of his scheme that he blamed the discrepancies on errors in Copernicus' tables! He modestly entitled his work "Mysterium Cosmographicum -- The Mystery of the Universe Explained". (Sounds like the New Age fog they carry at Borders, doesn't it? The two aren't much different.) The crucial illustration from his book is shown at left. The outer sphere represents the orbit of Saturn, and the central part (representing the inner solar system) is shown magnified at top right.Unfortunately, Kepler was barking up the wrong tree. There are no compelling geometrical reasons why the planets are at the distances they are from the Sun. If the solar system were to be disturbed in some way, for example if another star were to come close, the planetary orbits would change. Also, of course, we know now that there are nine planets, not six, and also an asteroid belt. But Kepler did not know this. To him, the solar system was the central, most important part of creation, and he felt the Creator would naturally come up with something very special for it, reflecting the eternal truths of number and geometric form.
In 1598, Kepler's school in Graz, along with other Lutheran institutions, was closed down by the young Archduke Ferdinand of Hapsburg, who had decided to cleanse the Austrian provinces of Lutheran heresy. Kepler was allowed to stay for a while, but the next year he was given the choice of embracing Catholicism or being expelled from Austria. Kepler wanted to go back to Protestant Tubingen, but they didn't want him, because of his known belief in Copernicanism. Tycho Brahe invited Kepler to come work with him, so Kepler left for Prague on January 1, 1600. Before he had ever met Brahe, he wrote to his mentor Maestlin:
"My opinion of Tycho is this: he is superlatively rich, but he knows not how to make proper use of it, as is the case with most rich people. Therefore, one must try to wrest his riches from him."When he began working with Brahe, Kepler realized it would not be so easy to use Tycho's data. Tycho was very secretive. He had his own agenda, which was to establish his own model of the solar system, the Tychonian, in which the Sun goes around the Earth once a year, but all the other planets go around the Sun. Brahe was not anxious for his data to be used to support a Copernican model. However, Kepler was pleased when Tycho suggested he work on the orbit of Mars, which has one of the least circular orbits, and hence would be a good test of new models, and for which Tycho would be obliged to give him a substantial amount of data. Kepler made a bet that he would understand the orbit in eight days -- but it would eventually take him eight years.
In 1601 Brahe's lifestyle caught up with him. He became very ill at a banquet, and a few days later died in agony of a bladder infection. Brahe's heirs were anxious to make as much money as possible out of the estate, and the impoverished Kepler realized that if he didn't act immediately, he would never get to use most of Brahe's data. As he wrote in a letter in 1605: "I confess that when Tycho died, I quickly took advantage of the absence, or lack of circumspection, of the heirs, by taking the observations under my care, or perhaps usurping them..."
Kepler set about trying to devise a system of the heavens based on these observations. On September 30, 1604, he was spurred on by the appearance of another nova -- Kepler's star. It was not quite as spectacular as Tycho's star, but it was spectacular enough. (Kepler's star is the last nova to be visible to the naked eye, by the way. Modern astronomers would become dangerously jubilant if they could observe such a thing, rather than the extremely dim and distant nova they've been obliged to make do with.)
After years of laborious calculations, Kepler finally realized that nothing he could do with circles would ever fit Tycho's data. And so, in one of the greatest leaps of imagination in the history of science, he put aside 2000 years of astronomical theory and began to search for some noncircular curve that would fit. First he tried an egg-shaped oval without success, then he settled on the ellipse.
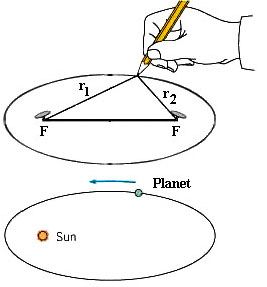 The ellipse is a flattened circle. Mathematically, an ellipse is defined by taking two points (called the foci), then generating a curve such that the combined distance from any point on the curve to each of the foci remains a constant. It is surprisingly easy to draw an ellipse: all you have to do is put a loop of string around two tacks stuck in a board, then keep the string stretched tight as you draw a curve around the tacks with a pencil. Since the total length of the loop of string cannot change, the length of string running from one tack to the pencil, then back from the pencil to the other tack, cannot change -- i.e., the combined distance is always constant, which is exactly the definition of an ellipse.
The ellipse is a flattened circle. Mathematically, an ellipse is defined by taking two points (called the foci), then generating a curve such that the combined distance from any point on the curve to each of the foci remains a constant. It is surprisingly easy to draw an ellipse: all you have to do is put a loop of string around two tacks stuck in a board, then keep the string stretched tight as you draw a curve around the tacks with a pencil. Since the total length of the loop of string cannot change, the length of string running from one tack to the pencil, then back from the pencil to the other tack, cannot change -- i.e., the combined distance is always constant, which is exactly the definition of an ellipse.Kepler found that the positions of Mars, as observed by Tycho, fit an elliptical orbit with a high degree of accuracy. It wasn't a very flattened ellipse, but it was most definitely not a circle. Furthermore, the Sun was located at one focus of the ellipse. Kepler eventually found that the orbits of the other planets could also be drawn as ellipses, with the Sun always at one of the foci. He announced this in his book "Astronomia Nova", published in 1609, and this is now known as Kepler's first law. The book also contained his second law: "A line connecting the planet and the Sun will sweep out equal areas in equal times as the planet moves about its orbit." This meant that the closer a planet was to the Sun, the faster it would move. Kepler went on later to apply these laws to the satellites of Jupiter as well.
Kepler's ellipses put an end to Greek astronomy. They abolished the celestial spheres that Eudoxus had placed in the heavens two thousand years before, and which even Copernicus had retained. Kepler's scheme of the solar system has been followed by astronomers ever since, without significant modification.
With the abolition of the celestial spheres, some other cause had to be found to explain the fact that the heavenly bodies remained in their orbits. The fact that the Sun was always at one focus of the elliptical orbit, that it was always in the plane of the orbit, and that planetary motion was faster the closer the planet was to the Sun, made it obvious to Kepler that the Sun somehow controlled the motions of the planets. He followed the notions of the English physicist Gilbert in thinking that some magnetic force was involved, but the systems he attempted to work out on such a basis were unsatisfactory. It was left for Newton to suggest a satisfactory explanation a half century later.
Kepler published another book in 1619, one that was particularly full of verbose mysticism. Kepler, aware of its difficulty, despondently suspected it might have to wait a century for a reader. In it, however, rather like a pearl in a mass of seaweed, was what is now called Kepler's third law, which stated that the square of the period of revolution of a planet is proportional to the cube of the distance from the sun. Again the Sun seemed to be the controller of planetary motion.
Kepler and Galileo carried on a friendly correspondence for a time, though they never met, and Kepler communicated his theories to Galileo. Galileo, however, in his book on the Copernican theory made no mention of Kepler's laws. He apparently felt they were to be regarded as little as Kepler's fantasies about regular solids and the music of the spheres -- to say nothing about his horoscopes. The correspondence broke off in 1610, and this may indicate a loss of sympathy between the two.
Nevertheless, when Galileo was constructing telescopes and sending them where he thought they would do the most good, one found its way to Kepler. Kepler used the telescope to observe Jupiter's moons -- which he had refused to accept until he saw them with his own eyes -- and promptly described them as "satellites," from a Latin term for the hangers-on of a powerful man. He began to work on the manner in which light waves were refracted by lenses. He managed to explain in this way how it was that telescopes -- and eyes too -- performed their function. He described an improved telescope in 1611, using two convex lenses in place of the one convex and one concave used by Galileo, and described, in theory, a compound microscope better than any then available. He also showed that a parabolic mirror focused parallel rays of light, a fact essential to the development of reflecting telescopes by Newton later in the century. Thus he founded the science of modern optics. But he was not able to deduce a general mathematical relationship to express the refraction of light. That was left for his younger contemporary, Snell.
In 1612 Kepler's protector, Rudolf II, died. The new emperor, Matthias, maintained Kepler in his position as court astronomer with a salary that was usually in arrears. Rudolf II had not been a prompt payer either. The Holy Roman Emperors were usually strapped for cash. In 1620 Kepler's mother, who dabbled in the occult, was arrested as a witch and, although not tortured, did not long survive her release, which was procured through her son's long-sustained efforts.
Kepler spent these years completing new tables of planetary motions based on Tycho's superlative observations and his own theory of elliptical orbits. He used the newly invented logarithms of Napier in his calculations, this being the first important use to which logarithms were put. Despite family troubles, financial difficulties exacerbated by the fact that Kepler fathered thirteen children, and continuing war and religious unrest, the tables, called the Rudolphine Tables in honor of Kepler's old patron, were published in 1627 and dedicated to the memory of Tycho Brahe. The work included tables of logarithms and Tycho's star map as expanded by Kepler. The Rudolphine tables immediately replaced all previous planetary tables in their unmatched accuracy.
Kepler's manuscripts were eventually bought by Catherine II of Russia over a century after his death and are preserved now at the Pulkovo Observatory in Russia.
This page is adapted from Michael Fowler's lectures and Web page at the University of Virginia, and Fred L. Wilson's lectures and Web page at the Rochester Institute of Technology.
A Ukrainian translation of this page is available here: Ukrainian