Waves



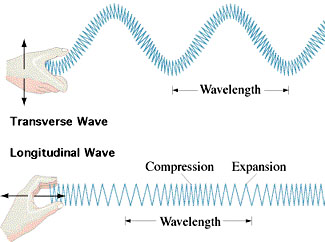
We have all seen waves (water waves, flags rippling in the wind, vibrations along ropes or strings), so we know what they are when we see them.  They are a disturbance propagating though a medium in such a way that the disturbance moves, but the medium itself does not.  Waves come in two varieties:  transverse and longitudinal.  For a transverse wave, the medium vibrates at right angles to the wave motion (example:  waves on a rope).  For a longitudinal wave, the medium vibrates in the same direction as the wave motion (example:  waves along a slinky).

Physicists characterize waves by three parameters:  amplitude, frequency, and wavelength.  The amplitude is the "height" of the wave, or in other words, a measure of the energy in the wave.  You find the frequency of a wave by counting how many wave crests pass a fixed point in a certain interval of time.  Frequency is usually measured in cycles per second, also known as hertz (Hz).  (That is, a 100 Hz wave has a frequency of 100 cycles per second.)  The wavelength is the distance from one wave crest to the next.

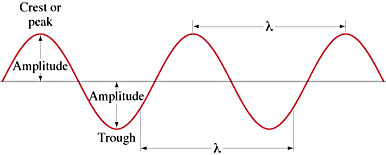
For sound waves, amplitude is related to the loudness of the sound, and frequency is related to the pitch.  The higher the frequency of the sound wave, the higher the pitch.  The speed of a sound wave through air at room temperature and pressure is about 343 m/s.  You can relate the speed of the sound wave to its wave parameters by:

v = f L

where:  v = the speed of the wave, f = the wave frequency, L = the wavelength.

For many types of waves, including sound waves, the speed of the wave through a medium does not depend too much on the frequency.  Sound waves of high frequency and low frequency move at pretty much the same speed through air -- that is, the sound from a tuba or from a dog whistle both travel at about 343 m/s.  Since the speed of sound is essentially constant, the equation above means that high frequency always implies a short wavelength for sound, and vice versa.

All waves carry energy and momentum, just like particles.  They can interact with matter, and transfer momentum, and cause heating to occur, and so forth.  Waves have several properties which are distinctly different from those of particles, however.  The most important ones are interference and diffraction.

Interference occurs when two waves are moving within the same medium.  For example, if one has two waves moving along a rope, one from the left and one from the right, they have to run into each other eventually.  When they do, it's obvious that any spot on the rope can only be in one place at one time, not two.  So, the rope responds to both waves at once, in a very simple way:  the amplitudes of the waves just add algebraically.  And once the waves are past each other, they keep right on moving in their original directions as though nothing had happened.  The figure below illustrates this.

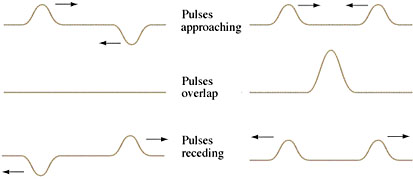In the left-hand set of three panels (going down), we see two wave pulses with opposite amplitudes approaching each other.  When they combine, their amplitudes cancel and there is apparently nothing left, since the rope is now a straight line.  But this is an illusion:  the energy and momentum of the waves cannot be disposed of that easily.  Though the rope may be straight for an instant, it cannot stay that way.  It is accelerating as it changes into and out of a straight line, and both waves reemerge from the straight line and continue onward with no change whatever.  The right-hand side of the graphic also shows two wave pulses colliding, except this time the pulse amplitudes are in the same direction, so when they meet the amplitudes add and temporarily create one large pulse.

In two or three dimensions, overlapping waves can create complex interference patterns, as can be seen in the wave patterns at a beach.  Even with only two wave sources, and only looking in two dimensions, the interference patterns are complex.
Diffraction is a more subtle wave phenomena than interference.  When a wave moving in two or three dimensions runs into an obstacle (let us say, a water wave striking a post sunk into a harbor), what happens depends on the wavelength of the wave.

If the wavelength is very small compared to the post, then the oncoming waves act more-or-less like particles, in the sense that points on the wave which just miss the post keep on moving, whereas points on the wave which impact the post are stopped.  In other words, a sharp shadow is created behind the post.  But if the wavelength is large compared to the post, then the waves begin "lapping around" the post and start to fill in the space behind it.  (Click here for a Quicktime movie illustrating this aspect of diffraction.)

If a wave encounters a wall with a gap in it, the result is the same as a wave encountering a post, except inverted.  If the wavelength is small compared to the gap, then the waves tend to beam through the gap in straight lines.  That is, they again act as a stream of particles would.  If the wavelength is large compared to the gap, however, then the waves radiate from the gap in all directions.  The graphic at right illustrates this:  the wavelength of the wave is equal for both barriers, but the left-hand barrier has a relatively large gap -- which means the wavelength is relatively small compared to the gap, so the waves tend to move ahead like particles would.  The right-hand barrier has a much smaller gap, so now the wavelength is large compared to the gap, and the result is nearly circular diffraction, very unlike particles.

Keeping track of when a wave will diffract and when it won't is easy if you think of it like this:  picture a wave as a fuzzy ball of fog, whose size is given by its wavelength.  If I take a wave with a wavelength = size of a baseball, and send it through a large doorway, then essentially the wave is too small to interact with the doorway and it goes on through much like the baseball would, i.e., in a straight line.  But if I try to send my baseball-sized wave through a hole just barely large enough to accept a baseball, then the fuzzy fog does interact with the opening, and the result is that the wave strongly diffracts, i.e., it radiates in all directions as it goes through the hole, very unlike a baseball.  Similarly, if my baseball-sized wave is directed towards the Hoover Dam, it will simply reflect from the dam like tossed rock would, because the dam is much too big for the wave to "feel" any edges.  But if I direct the wave towards a pencil-sized steel rod, then the wave is much bigger than the obstacle and so it will strongly diffract.  In this case, that means the baseball-sized wave will simply "lap around" the rod and keep on going, which is not what a solid baseball would do.

Diffraction accounts for the fact that you can hear around corners and also for the fact that pillars and other small obstacles do very little to impede the spread of sound in a room.  Sound waves at the frequency of human speech have wavelengths of roughly a meter, which means that they diffract around objects of household size and radiate when passing through openings even as large as a double door.  Light is also a wave, but you cannot see around corners nor through even the tiniest obstacle because light, unlike sound, has an extremely short wavelength -- less than a ten-thousandth of an inch.  This is so small that almost everything looks huge to a light wave, so it behaves like a classical particle and exhibits very little diffraction from objects of household size.


 Thermodynamics Timeline  |  Light & Sound 

 Ideas of Physics Homepage

A Ukrainian translation of this page is available here: Ukrainian