Plate 1: What An Electron Is
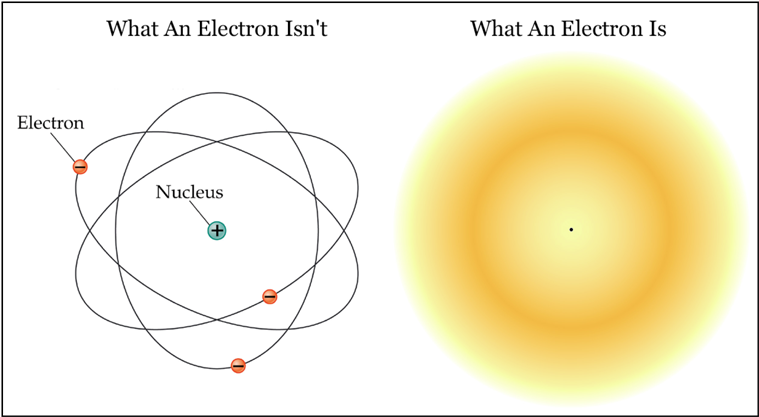
The most popular picture of the atom depicts it as a small nucleus (consisting of protons and neutrons) "orbited" by much lighter electrons. This picture tacitly assumes the electron to be a particle. Given that the electron has a precisely defined mass, a precisely defined electric charge, and several other precisely defined properties a bit too esoteric to discuss here, this assumption seems reasonable enough. The electron-as-particle is illustrated above at the left: it is shown to be a little ball orbiting the atomic nucleus much like the planets orbit the Sun, except with electrostatic force holding it in place rather than gravity. This picture has the advantage of being a very intuitive way to think about an atom. It has the slight disadvantage of bearing almost no resemblance to reality.
The illustration on the right is as close as one can get (with a two-dimensional drawing) to what an electron really is. The drawing depicts one electron "orbiting" one proton, represented by the tiny black dot at the center.1 The electron has assumed a form that can only be described as a cloud of probability. The electron possesses both kinetic energy and momentum, yet there is no motion. The cloud is perfectly static. The electron does not "orbit" the proton at all – it surrounds it like a fog. The most critical difference between a real electron and a classical particle is that a real electron does not exist in any one place. All it has is a certain probability of being here as opposed to there, which the illustration shows with darker and lighter colors (darker means more probable). If you decided to catch the electron using some kind of hypothetical scoop, then you could wave your scoop through the probability cloud and an electron might appear inside it – and then again, it might not. You could increase your chances by waving your scoop through the darker (higher probability) regions of the cloud, but in the end, statistical chances are all you have. There is no way to predict with certainty whether the electron cloud will interact with your scoop or not. It is critical to realize that this uncertainty is not because you are unsure of the electron's motion, and therefore don't know where to place your scoop. The electron is not like a buzzing fly hidden in the dark. It is not like a target moving so fast that you cannot track its location, or like a target hidden behind a smoke screen. The electron is a much more subtle object whose location can never be known for certain, because it does not have a specific location.
When we say that "the mass of an electron is 9.11 X 10-31 kilograms", what we really mean is that the total mass of any given electron probability cloud can only be 9.11 X 10-31 kg, or twice 9.11 X 10-31 kg, or three times, and so on2. If an old cloud changes into a new one, then its total mass, total electric change, and so on are just passed along. Thus, no matter what you do, enclosing one-quarter of an electron cloud inside your scoop will never get you one-quarter of an electron. It only gets you a 25% chance that all of the cloud will interact with your scoop, and thus that all of the mass of the electron will appear inside it.
Now, all of this is perfectly consistent with the notion that an electron does, in fact, have a definite position, and it is certainly much easier to think of an electron as a fly buzzing in the dark rather than as a slightly spooky "probability cloud". No less of an authority than Albert Einstein was always uncomfortable with the whole wave function/probability distribution/fundamental uncertainty "thing" which is central to quantum mechanics. As he once famously said, "God does not play dice". However, the indeterminacy of quantum mechanics comes straight from the basic mathematics of the theory, and as Niels Bohr famously replied to Einstein, "God not only plays dice, he throws them where they cannot be seen".
The theory of quantum mechanics can be reformatted, so to speak, such that the electron does have a specific, but unknown position, as opposed to being everywhere at once with differing probabilities. Such theories are called hidden variable theories, for the obvious reason. In most situations standard quantum mechanics and the hidden variable theories predict exactly the same thing, so there isn't much practical difference between the two. However, there are complicated, somewhat exotic situations in which they do not predict the same outcome, and physicists have examined these. The experiments are challenging to carry out, and one or two have in fact seemed to favor hidden variables over quantum mechanics. However, the great bulk of the experiments favor standard quantum mechanics, and as time goes by quantum mechanics is lengthening its lead over hidden variables. It would seem that the Universe is perfectly happy to be a place where "particles", at the most smallest and most fundamental level, simply do not exist.
1 The drawing is not to scale. If it were, the tiny dot would need to be 10,000 times more tiny to represent a real proton. At this scale, the dot would have a mass of about two kilograms, and the total mass of the yellow electron cloud would be about a gram.
2 When physicists say that an electron has "interacted" with something, what they really mean is that the electron has altered the shape of its probability cloud and shifted into a different quantum state. Solid objects move; electrons alter their probabilities. In our case, it would shift from the probability cloud illustrated for the hydrogen atom into one that would fit entirely inside your scoop. The shapes and transition rates of electron probability clouds can be calculated with astonishing precision, and thus the probabilities that characterize the electron are often known with the same certainty as the time of tomorrow's sunrise. To give an analogy, the quantum mechanics of many quadrillions of atoms is something like flipping a coin one million times. You know you will end up with pretty near 500,000 "heads" after a million coin flips, but you don't know what the coin will do on any particular flip. Likewise, the behavior of individual electrons cannot be predicted with certainty, but this represents no barrier to predicting (with great precision) the number that will be "heads or tails" when you're dealing with 1,000,000,000,000,000,000,000 of them.