The Sun's Evolution
The Hertzsprung-Russell Diagram (aka the Main Sequence)
Most stars are rather simple things. They come in a variety of sizes and temperatures, but the great majority can be characterized by just two parameters: their mass and their age. (Chemical composition also has some effect, but not enough to change the overall picture of what we will be discussing here. All stars are about three-quarters hydrogen and one-quarter helium when they are born.)
The dependence on mass comes about because the sheer weight of the star's mass determines its central pressure, which in turn determines its rate of nuclear burning (higher pressure = more collisions = more energy), and the resulting fusion energy is what drives the star's temperature. In general, the more massive a star is, the brighter and hotter it must be. It is also the case that the gas pressure at any depth in the star (which also depends on the temperature at that depth) must balance the weight of the gas above it. And finally, of course, the total energy generated in the core must equal the total energy radiated at the surface.
This last fact generates yet another constraint, because the energy radiation of a sphere suspended in a vacuum obeys a law known as the Stefan-Boltzmann Equation:
Here L is the luminosity of the star, C is a constant1, R is the radius of the star in meters, and T is the surface temperature of the star in K°. Note how swiftly the energy radiated by a star rises with T: doubling the temperature causes its energy output to increase by 16 times.
A star which meets all these constraints is said to be in hydrostatic equilibrium. Hydrostatic equilibrium has the fortunate effect that it tends to make stars stable. Should a star's core be compressed, the compression causes nuclear burning to increase, which generates more heat, which forces up the pressure and makes the star expand. It goes back to equilibrium. Likewise, if a star's core should be decompressed, then nuclear burning decreases, which cools the star and brings the pressure down, and thus the star contracts and again returns to equilibrium. The energy output of the Sun has not fluctuated by more than perhaps 0.1% to 0.2% in human history – not bad for a nuclear reactor that has no regulatory committee, no engineers, and hasn't had a safety check in nearly five billion years.
Navigation Menu
Introduction
Matter Under Pressure
The Birth Of The Sun
The Sun's Evolution
The End Of The Sun
How Large Stars Evolve
The Other Type Of Supernova
After The Supernova
1 – Very well, if you must know, the constant is equal to 5.67 x 10-8 W m-2 K-4.
This equation is important because it demonstrates how even small changes in the surface temperature of a star can lead to large variations in energy output. If the Sun's temperature was just raised from 5780 K° to 5900 K°, its luminosity would rise by nearly 9%.
The tight interrelation of temperature, pressure, mass, and rate of nuclear burning means that a star of a given mass and age can only achieve hydrostatic equilibrium at one set of values. That is, every star in our galaxy of the same mass and age as the Sun also has the same diameter, temperature, and energy output. There is no other way for everything to balance. If one generates a very hard-core astrophysics graph known as a Hertzsprung-Russell Diagram (H-R diagram for short), the relationship between a star's mass and its other properties becomes more clear. An H-R diagram is shown in Figure 1.

The main sequence exists precisely because of the inflexible nature of hydrostatic equilibrium. Stars with very low masses (as little as 7.5% that of the Sun) lie at the lower right of the H-R diagram. They must lie at the lower right. This part of the H-R diagram corresponds to extremely low luminosity – as little as a ten thousandth that of the Sun – and low surface temperature, equivalent to the dull orange-yellow glow of molten metal. These stars do not have enough mass to create the pressure necessary to make the nuclear burning in their cores go any faster. High-mass stars (upwards of 40 solar masses) reside at the upper left, as they must. Contrary to the low-mass stars, their immense masses and high central pressures give rise to giants that can be 160,000 times more luminous than the Sun, and so hot that they give off more energy in the ultraviolet than they do as visible light. The Sun lies almost exactly halfway between these extremes, and thus it is neither extremely dim nor extremely bright as stars go. It shines with a bright yellowish-white color.
The one-to-one nature between mass and hydrostatic equilibrium means that as you vary the mass of a star, all you can do is slide along a single, predetermined track with respect to all its other physical properties. This track is exactly the main sequence. But now that I've said that, a second look at the H-R diagram reveals that there is a smattering of stars well off the main sequence: they are concentrated in "islands" at the upper right and lower left. Since the stars at the upper right are very luminous yet nonetheless have cool, reddish surfaces, astronomers call them red giants. Similarly, since the stars at the lower left are very dim yet also white-hot, they are called white dwarfs. We have met the white dwarfs already, in a theoretical way. Now let's see where the real ones come from.
2 – Astronomers traditionally classify main-sequence stars with letters, like so:
O - 30,000 to 40,000 K°
B - 10,800 to 30,000 K°
A - 7240 to 10,800 K°
F - 6000 to 7240 K°
G - 5150 to 6000 K°
K - 3920 to 5150 K°
M - 2700 to 3920 K°
Within each class, numbers from 0 to 9 provide subclasses, with zero being the highest subclass (highest temperature). The Sun is classified as a G2 star.
Red Giants And White Dwarfs
Red giants and white dwarfs come about because stars, like people, change with age and eventually die. For people, the cause of aging is the deterioration of biological functions. For a star, the cause is the inevitable energy crisis as it begins to run out of nuclear fuel.
Since its birth 4.5 billion years ago, the Sun's luminosity has very gently increased by about 30%.3 This is an inevitable evolution which comes about because, as the billions of years roll by, the Sun is burning up the hydrogen in its core. The helium "ashes" left behind are denser than hydrogen, so the hydrogen/helium mix in the Sun's core is very slowly becoming denser, thus raising the pressure. This causes the nuclear reactions to run a little hotter. The Sun brightens.
This brightening process moves along very slowly at first, when there is still ample hydrogen remaining to be burnt at the center of the star. But eventually, the core becomes so severely depleted of fuel that its energy production starts to fall regardless of the increasing density. When this happens, the density of the core begins to increase even more, because without a heat source to help it resist gravity, the only possible way the core can respond is by contracting until its internal pressure is high enough to hold up the weight of the entire star. Bizarrely, this emptying of the central fuel tank makes the star brighter, not dimmer, because the intense pressure at the surface of the core causes the hydrogen there to burn even faster. This more than takes up the slack from the fuel-exhausted center. The star's brightening not only continues, it accelerates.
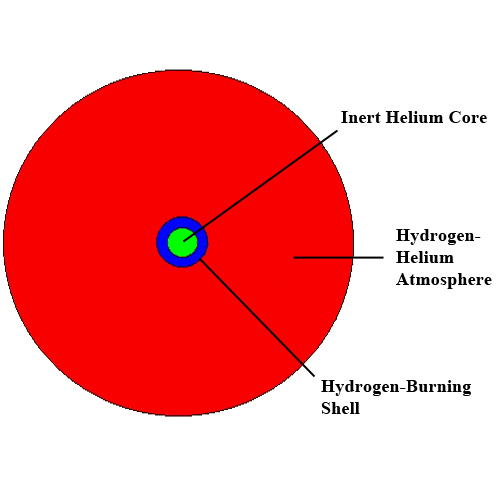
The Sun is about half-way through a very long process of shifting from a mode where hydrogen is burned in a kernel at its center to a mode where hydrogen will be burned in a spherical shell wrapped around an intensely hot, very dense, but quite inert, helium core. Once it makes the transition from core burning to shell burning, it will be entering its twilight years. As the helium core grows, so does the hydrogen-burning shell above it, thus making the Sun ever brighter even while ominously increasing the rate at which helium is accreted onto the core. The growing core burns the Sun's hydrogen yet more rapidly, which in turn only enlarges the core more rapidly. . . .
In short, in the end, the nuclear furnace at the center of every star begins to overheat. To put numbers on this, when the Sun was formed 4.5 billion years ago it was about 30% dimmer than at present. At the end of the next 4.8 billion years, the Sun will be about 67% brighter than it is now. In the 1.6 billion years following that, the Sun's luminosity will rise to a lethal 2.2 Lo. (Lo = present Sun.) The Earth by then will have been roasted to bare rock, its oceans and all its life boiled away by a looming Sun that will be some 60% larger than at present.4 The surface temperature on the Earth will be in excess of 600 F°. But even this version of the Sun is still stable and golden compared to what is to come.

4 – Alas, the feedback loops mentioned in footnote 3 cannot protect the Earth forever. Once its greenhouse effect has dropped to zero, the Earth cannot do anything more to cool itself.
Around the year 7.1 billion AD, the Sun will begin evolving so rapidly that it will cease to be a main-sequence star. Its position on the H-R diagram will begin to shift from where it is now, near the center, towards the upper right where the red giants live. This is because the Sun's helium core will eventually reach a critical point where the pressure from normal gasses cannot hold up the crushing weight being piled on it (not even gasses heated to tens of millions of degrees). A tiny seed of electron-degenerate matter will begin to grow at the center of the Sun. The details of this transition are subject to debate, but theoretical calculations indicate that it will begin when the Sun's inert helium core reaches about 13% of a solar mass, or about 140 Jupiters.
At this point in its life, the Sun will become unruly. The mechanism that has been slowly making it brighter for the past eleven billion years – more core pressure, yielding hotter nuclear burning, yielding more helium to enlarge the core – is now accelerated to disastrous levels by the steadily increasing electron-degeneracy. 500 million years after it hits the critical point, the Sun's luminosity will balloon to 34 Lo, fiery enough to create glowing lakes of molten aluminum and copper on the Earth's surface. In only 45 million years more it will reach 105 Lo, and 40 million years after that it will leap to an incredible 2,300 Lo.
By this time the enormous energy output of the Sun will have caused its outer layers to inflate into a vast but very tenuous atmosphere at least the size of the orbit of Mercury, and possibly as large as the orbit of Venus. (Think of how violently the water behaves in a pot of rapidly boiling water as compared to that in a gently simmering pot. This is analogous to why the Sun's atmosphere "boils" outward as its core becomes hotter.)5 The huge size of the solar atmosphere and the enormous heat output of the Sun mean that: #1) the Earth will have been burnt down to nothing but a seared iron core by this point, if not vaporized altogether – calculations show that it could go either way – and #2) the solar atmosphere will be relatively cool despite the Sun's tremendous energy output. Thus, the Sun will be both red in color and extraordinarily luminous. It will have joined the red giants. (See Figure 2.)
5 – But it is not a very good analogy. Click here to read the full story, or click the icon.

For a translation of this page into other languages, click a link below.
Catalan, Croatian, Estonian, Finnish, Georgian, Irish Gaelic, Marathi, Norwegian, Polish, Russian, Serbian, Spanish, Turkish, Ukrainian