A Star Is Born
The hydrogen and helium are remnants of the Big Bang; the 1% of "dirt" comes from the stars themselves and we will discuss this interesting bit of self-enrichment later. The term "Big Bang" was originally coined as a term of derision by British astronomer Fred Hoyle, who was not an avid believer in apocalyptic cosmic explosions. However, it was so descriptive that it stuck and became the proud name for a whole set of cosmological theories based on the idea that all the mass and energy in the Universe originally exploded out of a quantum fluctuation 1030 times smaller than a proton. Recent precision work using cosmic microwaves places the Big Bang at 13.7 billion years ago. The observed abundances of hydrogen and helium isotopes2 in interstellar clouds have been carefully compared to calculations of which isotopes should have been created in the few hours following the Big Bang, and the agreement is very impressive. This essentially proves that the Big Bang could not have produced any elements in quantity other than hydrogen and helium, and it also provides powerful verification for the Big Bang itself.
Most of the original hydrogen and helium generated by the Big Bang has long ago collapsed into stars. The Milky Way galaxy consists of perhaps 10% gas and 90% stars at this point. However, 10% of a galaxy is still a lot of gas, enough to make about 30 billion Suns, so there is no lack of newborn stars for us to observe. (See Plate 5 for more information on star-forming clouds.) And as always when discussing the stars, the first question is: how will the clouds behave as they are compressed by gravity?
In this case, we are in the realm of the ultra-tenuous rather than the ultra-compressed. The atoms in an interstellar cloud are so far apart that they rarely encounter each other during the initial stages of collapse. You can think of them as acting like raindrops falling towards the cloud's center. Similar to Earthly raindrops, they pick up speed as they fall. This kinetic energy is eventually converted into heat as they begin to strike one another inside the ever-shrinking interstellar cloud. (The heating effect is quite parallel to what happens inside the piston of a Diesel engine during the compression cycle, if you have any familiarity with automotive mechanics.) About half of the heat is radiated away during the cloud's contraction; the other half remains trapped inside the proto-star. At the start of the collapse, the temperature of the gas cloud is normally very frigid, only a few degrees Kelvin (about -450 F°), and it is initially several light-years across. By the end, it will have shrunk to a few million miles in radius – a volume reduction of some 1018 times – and its surface temperature will have reached about 4,000 K°. The temperature at its core is typically above ten million K°.
A newborn star is thus a very hot, luminous object – as were the planets in our Solar System, once upon a time, because planets are essentially born from the same collapsing interstellar matter as their parent stars. The critical difference between newborn stars and planets is this: a planet just cools off after it forms, but a star is so massive that the escalating temperature and pressure at its core ignite nuclear reactions, and it begins producing energy.
Introduction
Matter Under Pressure
The Birth Of The Sun
The Sun's Evolution
The End Of The Sun
How Large Stars Evolve
The Other Type Of Supernova
After The Supernova
1 – A light-year is the distance light travels in one year. Many people believe that a light-year is a unit of time, but it isn't. It is a unit of distance. The speed of light is 186,282 mi/sec, so a light-year is (186,282 mi/sec) x (sec/yr) = 5.878 trillion miles. Astronomers also use light-minutes (the distance light travels in a minute), light-hours, etc. The distance between the Earth and the Sun is thus 93 million miles or 8.3 light-minutes, as you wish.
2 – Isotopes are nuclei with the same number of protons (they are the same element) but with different numbers of neutrons. Isotopes are designated by putting a number on the element's name: i.e., carbon-14, where the 14 means that the number of protons plus neutrons equals 14. Hydrogen is an exception: hydrogen-2 is called deuterium, and hydrogen-3 is called tritium.
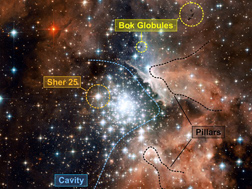
Plate 5
The Energy Source Of A Star
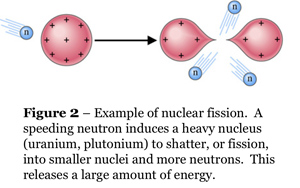
By definition, a star is an object that "burns" hydrogen via nuclear fusion. This pathway for liberating nuclear energy is different from that used by humans for submarines, electricity, and so on. We use nuclear fission. The fission pathway takes advantage of huge, bloated, radioactive nuclei at the end of the Periodic Table of the Elements, such as uranium or plutonium (elements #92 and #94). Nuclear fission is illustrated in Figure 2. When heavy nuclei are fissioned (or smashed) into lighter nuclei such as barium or krypton, they literally explode, yielding enormous amounts of energy. The fission nuclear-energy pathway is somewhat akin to shattering a tank of explosive chemicals.
Nuclear fusion operates in exactly the opposite direction: very light and perfectly stable nuclei at the start of the Periodic Table are fused (combined) into heavier nuclei, providing an energy release even more enormous than that of nuclear fission. Like most stars, the Sun fuses the very lightest element, hydrogen, into the second lightest, helium. Hydrogen has an atomic weight of one, and helium has an atomic weight of four, so this means that four hydrogen nuclei must be fused to make one helium nucleus. How does this come about? Is there a hideous hydrogen train wreck where four hydrogens collide in the same place at the same time?
Not exactly. That would be extremely improbable. Hydrogen fusion occurs in steps, like so:
Step 1) Two protons, aka hydrogen nuclei, collide. It happens to be impossible for two protons to fuse with each other (their electrostatic repulsion is too great), but not to worry. Now and then, before the colliding protons can separate, nuclear forces3 cause one of the protons to turn into a neutron! As I mentioned earlier (in the previous section), protons and neutrons have their own quantum states. What I didn't tell you is that the proton and the neutron are quantum states, and therefore can swap identities! No fooling4. The nucleus that results from the collision is thus a proton-neutron pair. This is an isotope of hydrogen that could be called hydrogen-2, but physicists usually call it deuterium. In symbols, where p represents a proton and n represents a neutron, the reaction is: p + p ---> np + energy + (other particles called neutrinos that don't concern us here; I will discuss them later).
Step 2) A proton collides with the deuterium. It sticks, giving us 2 protons + 1 neutron = helium-3. In symbols:
np + p ---> ppn + energy.
Step 3) Two helium-3 collide. In the resulting fireball, the helium-3 nuclei rearrange themselves into one helium-4 and two protons. In symbols: ppn + ppn ---> pnpn + p + p + energy. Fusing a proton to the helium-3 might seem a more likely third step, but that would create ppn + p ---> pppn, which is lithium-4, not helium-4. Lithium-4 is so unstable that it almost disintegrates before it is created, thus this reaction path contributes virtually nothing to the Sun's energy output.
4 – Quarks are sub-nuclear particles which form, among other things, the proton and the neutron. Quarks are quite happy to exchange identities, like actors changing costumes, and will do so at the drop of a hat unless prohibited by a lack of energy. Case in point, the proton is the only combination of quarks that is stable as a free particle, for the simple reason that it is the lightest (least energetic) quark combination possible. Since the quarks cannot form a different combination unless energy is added, the proton cannot change unless it is involved in a violent collision. Once fusion is initiated, however, the quarks can change, and thus it is possible for a proton to suddenly become a neutron.
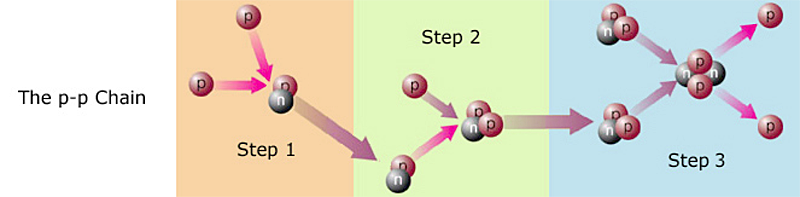
The net result is that four hydrogens have become one helium. This three-step process is called the p-p Chain, and is illustrated above. It is the primary energy source for most stars.
One might wonder why ConEd, the U.S. Navy, etc, use nuclear fission rather than nuclear fusion, given that: 1) fusion produces more energy, 2) fusion burns hydrogen = H2O = water for fuel, whereas fission uses rare, expensive, radioisotopes, 3) hydrogen fusion produces far less radioactive waste than fission, since its reaction product is non-radioactive, and 4) fusion processes cannot have "meltdown" accidents like fission can.
The simple answer is that nuclear fusion is terribly difficult to initiate. With fission, all one needs is a single nucleus that is already unstable (i.e., radioactive), and then you can "shatter" it with a tap from a speeding neutron as shown in Figure 2. Neutrons have no electric charge, thus there is nothing to stop them from approaching any atom. With fusion, you must take nuclei that are light, stable, and worst of all, positively charged, and convince them to come together. The nuclei electrostatically repel each other ferociously, and the more closely they come together, the more ferociously they repel. (See Plate 6 for an illustration.) Because nuclear forces have very short ranges, they can only overcome the electrostatic repulsion and initiate fusion when the nuclei are literally on top of each other. The atoms in the fusing gas therefore must be moving at terrific velocities to make such a close approach, i.e., the gas must be raised to terrific temperatures and pressures before you have any hope of getting any energy out of it.
Plate 6
At present, the only way we have of initiating hydrogen fusion is to use nuclear fission: the so-called "hydrogen" bomb uses the explosion of a plutonium bomb to (very briefly) ignite uncontrolled fusion of the hydrogen isotopes deuterium and tritium. We cannot control fusion, although much research on the subject has been conducted over the past 40 years. The Sun dodges these problems and fuses hydrogen via its sheer, overwhelming bulk. The pressure at its center squeezes the gas there to fourteen times the density of lead. The temperature is 15 million K°.
Yet, as extreme as those numbers are, they still are not large enough to ignite rapid hydrogen fusion. In fact, they are just barely large enough to ignite any hydrogen fusion at all! You may well wonder what I mean by "barely", given how bright the Sun is, and I mean this: the Sun has been shining for 4.5 billion years,5 yet it has only burnt 5% of its hydrogen fuel! If you never drove your car, but just opened the gas cap for one second each day to let some fumes escape, you'd be using your fuel faster than the Sun does. It is hard to achieve fusion. Here are some numbers to illustrate what I mean:
A) The Sun's luminosity (total power output) = 3.86 X 1023 kilowatts. At current global consumption levels, it would take the world's population 792,000 years to use the energy produced by the Sun in one second. Astronomers denote this amount of power as Lo, or one solar luminosity.
B) The energy produced by the nuclear fusion of one kilogram (two pounds, 3 ounces) of hydrogen is 177,720,000 kilowatt-hours (!!). This represents enough electricity to run the average American household for 3000 years.
C) Dividing the solar luminosity (A) by the energy yield from one kilogram of hydrogen (B) tells us how many kilograms of hydrogen must be burnt each second to power the Sun: 603 billion. To mine this much tonnage, you would need to excavate the entire state of Illinois to a depth of 1000 feet, per day. Approximately.
D) The Sun's mass is 1.99 X 1030 kilograms = 332,900 times the mass of the Earth. Dividing this into the 603 billion kilograms calculated in (C) gives us the fraction of the Sun that is being burnt each second: 3 X 10-19. This is about the same ratio as comparing one penny to the gross economic product of the entire world for the next 1,000 years. Thus we see how the Sun paradoxically manages to radiate so much energy and yet burn (almost) no fuel, relative to its size. Its immense mass translates even nanoscopic percentages of hydrogen burning into the equivalent of millions of H-bombs exploding per second.
So, in summary, stars like the Sun use the pressure of super-heated gasses to hold off the relentless force of gravity. Even better and more fun (if you are an astronomer), the heat source for the gasses is a natural nuclear reactor. This means that stars are way more violent and dynamic than planets are, and in the following section we will consider some of the ramifications of this.
5 – In case you are wondering where this number comes from, it comes from astrophysical theory, the age of the Earth as determined from geophysical considerations, and most accurately of all, from radioactive dating of the oldest known meteorites.
For a translation of this page into other languages, click a link below.
Bosnian, Croatian, Estonian, Georgian, Kazakh, Norwegian, Polish, Russian, Spanish, Ukrainian