The Life And Death Of Stars
Matter Under Pressure
To understand the stars, you must understand pressure. From birth to death, the internal pressure of a star created by its own weight is the most dominant factor in the star's life.
Suppose you take a pile of sand, and add more sand to it. The pile will become larger. One might imagine that this is also true for planets or stars, and it is – but only to a point. The thing is, what we call "solid matter" is nothing of the sort at microscopic scales. Matter consists of tiny atoms. If you could expand the nucleus of an atom to the size of a marble, then it would weigh three billion tons and the next-nearest nucleus would be two miles away. Between the nuclei there are only lightweight electron "clouds". (See Plate 1 for more information about electron probability clouds.)
Billion-ton, half-inch marbles scattered miles apart equals a lot of empty space, not solid matter. The factor that makes matter "solid" is the electromagnetic force operating between the atoms. This force, plus the rules of quantum mechanics, lock the atoms into the arrangements that we humans are pleased to call "solid", mostly because they can resist any compressional force that our technology can bring to bear. But, they're not. Nothing is solid if you apply enough pressure to it. The idea that more mass must equal a larger volume is true only for "small" objects like planet Earth, whose weight is not enough to compress their cores too much. (However, even for smaller planets such as Mars or the Earth, the central pressures are still immense. Earth has a volume about 20% less than one might expect it to have, based on its chemistry, because its weight has compressed its central iron core to about double the density of iron found on the surface.)
Navigation Menu
Introduction
Matter Under Pressure
The Birth Of The Sun
The Sun's Evolution
The End Of The Sun
How Large Stars Evolve
The Other Type Of Supernova
After The Supernova
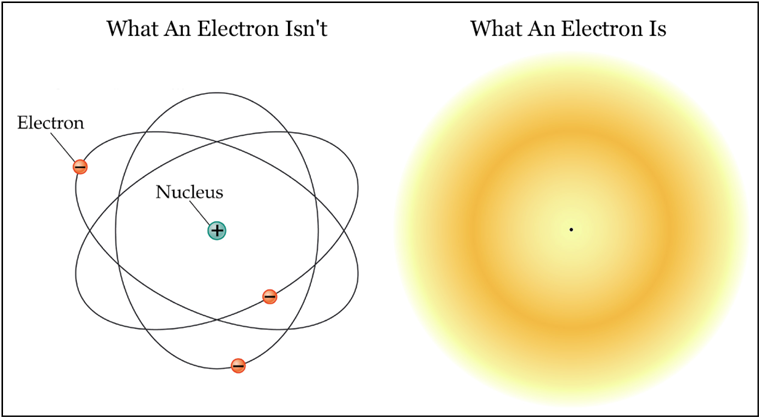

Plate 1 Plate 2
As planets become more massive, the tendency towards gravitational compression increases until eventually, at a mass roughly 1.7 times that of Jupiter1 (540 Earth masses), one reaches a critical point where the planet stops getting larger! Beyond this critical point2, adding more mass to a planet actually makes it smaller because the compression created by the extra mass is greater than the volume of the extra mass. (Plate 2 has more details.)
2 – For the purists, this theoretical maximum depends on several assumptions, such as whether the planet is made up mostly of hydrogen and helium, or not. For our purposes, an estimate of 1.7 Jupiter-masses is good enough.
Because super-massive planets combine decreasing radius with increasing mass, their densities (mass divided by volume) are stratospheric, many times that of lead. The central temperatures and pressures of super-massive planets are so immense that atoms cannot bond to each other, i.e., rocks and ice and other compounds cannot exist. All you can have are individual atoms floating about. It is thus more accurate to think of super-planets as extremely heavily compressed balls of gas, rather than as a liquid or solid core with an atmosphere wrapped around it. Core pressure also limits how massive a planet can be: the very dense, bluish planet illustrated in Plate 2 has a mass right at the edge of where you can squeeze on a ball of cold gas and still expect it to behave like a ball of cold gas. The upper left of the plate illustrates the marvelous result if you move beyond this, to about 75 Jupiters (24,000 Earth masses): hydrogen fusion is ignited and the "planet" begins to shine! It has become a dwarf star.
We will discuss what hydrogen fusion is, and how it generates copious amounts of nuclear energy, a bit later on. The important point here is that the generation of heat deep inside the planet/star radically transforms it. Inert super-planets just shrink as you pile on more mass, but the heat in a star dramatically raises the pressure of its gasses and halts any further contraction. Indeed, the vast energy output of larger stars such as our Sun causes them to swell into huge (albeit light and fluffy) balls far more imposing than any planet. (See Plate 3 for more information about the Sun.)
However, the Sun and other stars can maintain their volume only so long as they have a heat source to generate high-pressure gas, and no heat source can last forever. Since gravitational compression is what we are interested in at the moment, let us brush aside heat generation as a mere temporary roadblock and move on. Suppose we have a 75 MJ planet/star which cannot generate heat. What happens in that case, as we add more mass?

Plate 3
It continues to shrink, of course. To make a long story short, massive objects (with no heat source) never stop shrinking as they grow more massive. But, as they move into the realm of 100 Jupiter masses or so, they do change the way that they shrink.
As the atoms in a star are pressed more closely together, they eventually reach a point where the electron clouds from adjacent nuclei begin to overlap. This causes the physics of the star to take a sharp turn into very odd territory, because it means that quantum mechanics is now calling the shots rather than classical physics. The fact that electrons are really clouds and not solid objects (see Plate 1) might lead you to believe that it would be easy to squeeze electrons together – and you would be quite wrong. Electrons are quantum mechanical clouds, not puffs of air, and as it happens, quantum mechanics severely disapproves of overlapping electron clouds. (This disapproval is technically known as the Pauli Exclusion Principle, after physicist Wolfgang Pauli.) It is not easy to condense a discussion of quantum mechanical theory into a few paragraphs, but fortunately, we only need to cover a few key points.
All You Need To Know About The Quantum Mechanics Of Stars
Atoms are made of protons, neutrons, and electrons. Protons and neutrons form the nuclei of atoms and are very dense, weighing in at an incredible 1018 kg/m3. (If the entire Earth were compressed to proton/neutron densities, it would only be about 700 feet across.) Atomic nuclei thus behave like very tiny but very heavy particles. Electrons are a different kettle of fish. Far less dense than protons or neutrons (by a factor of 1013), electrons are usually said to "orbit" atomic nuclei by popular writers, even though most of us in the physics community dumped the notion of point-particle electrons back in 1927. As elaborated in Plate 1, electrons are not particles as such. They are more complex entities which act like waves most of the time, yet carry discrete mass and momentum as though they are particles.
Now, quantum mechanics is called quantum mechanics because elementary particles like the electron are normally constrained to occupy energy and momentum states (or energy levels, if you will) that exist only at specific quantized values. Only elementary particles moving freely in space, interacting with nothing, can take on any energy in the same way that a car on the highway can take on any speed. For an electron inside an atom, the possible energy states it can occupy are analogous to a crate setting on a staircase. (See Figure 1 at right.) The crate can be on one step, or the next, but it cannot rest anywhere in between. Like the crate, an electron can spontaneously bounce "down" the staircase to a state of lower energy, but it can never move "up" the stairs without an input of energy from outside. Unlike the crate, however, the electron will always move downward sooner or later, with or without outside help. And very unlike the crate, it is impossible to predict when the electron might do this: all you can do is specify a probability for how long it might take. (If you wish to push the crate/stairs analogy to the extreme, then you can imagine a crate with an agitated rabbit locked inside. You know the wobbling crate will fall down the stairs eventually, but you don't know when.)
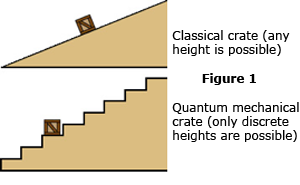
Another way an electron differs from a crate is that two crates are happy to set on the same step, but two electrons aren't. Simply put, two electrons can never occupy the same quantum state. They may and frequently do occupy the same space, but that's different. (Imagine two clouds of smoke from different cigars, mixing in the air. That's what I mean when I say two electrons can "occupy" the same space. They can both have some probability of being at the same point.) What electrons may not do is occupy the same space and simultaneously possess the same energy and momentum. In other words, if clouds of cigar smoke really behaved like electrons, then smoke clouds of the same temperature and color would be required to bounce off each other like rocks rather than mix! They could only mix if they were at different temperatures or had different colors. If this seems a bit odd – well, I said it wasn't easy to explain quantum mechanics in a few paragraphs. The main point here is that electrons obey an exclusion rule which forbids them from occupying the same quantum levels.
Normally, however, this exclusion rule only applies to electrons that are within the same atom. For "normal" matter (like the kind you are made of), the electrons are attached to nuclei which are littered across the space within you like so many marbles scattered miles apart. There is plenty of room for the small family of electrons in each atom to have the most favorable – that is, the lowest energy – states all to themselves. (See Plate 4 for an illustration.)
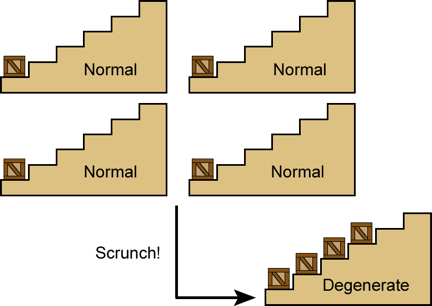
Plate 4
This happy arrangement comes to an end as the electron clouds start to overlap inside a collapsing star. As an increasing percentage of them are crushed together, the rules of quantum mechanics demand that only one of the trillion trillion trillion jostling electrons in a cubic centimeter remain in its original, lowest-energy state. Think of it like urban housing: if the population density is low enough, every family can live in a ranch-style house. But when the density reaches that of Manhattan, then someone has to live 62 stories off the ground. Electrons are rather like this, except worse. In the quantum version of Manhattan, only one electron in the entire city is allowed to live on the ground floor! The other electrons must be pushed into higher energy states, and since there is only one electron per state no matter how many electrons there are, the electrons quickly soar to astonishing energies. On average the electrons in a collapsed star carry 100,000 volts of energy, which corresponds to an "electron temperature" well above one billion degrees Kelvin3 if you think of the electrons as just the particles in a hot gas.4 (That is, 100,000 volts is far more than enough to rip the electrons away from individual nuclei, so the electrons are free to wander from one side of the star to the other like a gas.) The matter is said by physicists to have condensed into a new and peculiar state called electron-degenerate matter.
4 – Heat is simply the random motion of small particles. The more energetic the motion of the individual particles, the higher the temperature of the whole.
At this point our star has perhaps a quarter of a solar mass (roughly 80,000 Earth masses), packed into a volume not much more than double the Earth's radius. It is now so dense that a one-quart bottle of the electron-degenerate matter near its surface would weigh 50 tons. Such objects are by no means theoretical: the Milky Way galaxy contains possibly ten billion of them, and the first one was sighted in 1862. Astronomers refer to them as white dwarfs, because they are very small and white-hot. (Pride obliges me to note that the telescope in Northwestern's Dearborn Observatory was the very instrument used to make the historic 1862 sighting! Honesty forces me to admit that Northwestern did not acquire the telescope until 1887; in 1862 the telescope was still in Boston, where it was manufactured.)
For normal matter – gas, liquid, or solid – one envisions atoms as miniature solar systems, with clouds of "planetary" electrons surrounding nuclear "suns". A few electrons are allowed to behave like trolley cars and can be shared between neighboring atoms to form chemical bonds, but that's all. For electron-degenerate matter, as you might imagine, this "solar system" picture does not work at all. The electrons in degenerate matter are compressed so closely together that they more-or-less behave as if the entire star is one huge quantum system. They form an electron gas, and behave very much like a highly pressurized fluid inside the star. The electron-naked nuclei behave less like "suns" and more like lead shot zipping through the electron gas.
Surprisingly, the motion of the nuclei is almost completely unaffected by this change in their electron entourage. They still move as though they are in a normal gas rather than an electron-degenerate one. There are two reasons for this. First, nuclei aren't electrons. Rules that ration electron energy are completely irrelevant to the protons5 and neutrons6 that make up nuclei. (Protons and neutrons have their own quantum states, thank you.) Secondly, the nuclei are much denser and more massive than the electrons. As the nuclei move, they are as oblivious to the energy states of the electrons as a cannonball is to atmospheric humidity.
6 – Neutrons have almost exactly the same mass as protons (neutrons are 0.06% more massive) but have no electric charge, hence the name. Ordinary matter consists of about 50% protons and 50% neutrons, so neutrons locked inside nuclei constitute about half of the normal matter in the Universe. However, very unlike protons, free neutrons are not stable. Outside the nucleus, neutrons decay into a proton, an electron, and something called an anti-neutrino, in about 10.6 minutes. Free neutrons were not detected until 1932.
What this means is, if you heat or cool electron-degenerate matter, then the nuclei move faster or slower just as they would in a normal gas. But unlike a normal gas, the electrons don't care and don't follow suit. They are not attached to any particular nucleus any longer and in fact, the only factor that has any effect on them is the struggle to push themselves farther apart and avoid the exclusion rule. That struggle results from the immense compression created by the immense gravity of the white dwarf, and gravity has nothing to do with temperature. Thus, the electron gas responds only to changes in the mass of the white dwarf (i.e., to changes in its gravity), and not to changes in its temperature, which in turn means that a white dwarf does not change in size at all as it is heated or cooled.
That last fact is a very critical one, as we shall see later. Normal gases change volume when they are heated or cooled, which is why hot air rises and cooler gas falls. But electron-degenerate matter behaves more like an exotic, fantastically dense liquid than it does a gas, and liquids do not change volume much when they are heated. They only get hotter. Hence electron-degenerate matter is much more difficult to compress than normal matter. (It takes energy to elevate an electron to a higher level, and elevating all the electrons in something with the mass of a star takes lots of energy.)
In short, when it comes to how they react to increased pressure or temperature, white dwarfs behave more like "solid" bodies such as the Earth than they do like gaseous bodies such as Jupiter or the Sun. We have almost come full circle in our discussion of massive bodies.
Almost.
In 1931, theoretical astrophysicist Subrahmanyan Chandrasekhar (then only 21 years old) published a trio of startling papers on electron-degenerate matter. His calculations showed that as a white dwarf becomes more massive it must inevitably approach a critical point. This turns out to be a consequence of Einstein's theory of relativity, and since I cannot explain relativity in a paragraph, I will just outline the facts: As the electrons in a white dwarf are lifted to higher energy levels, they move faster. However, one of the most fundamental laws of relativity is that nothing can move faster than the speed of light (186,282 miles per second). As particles approach this speed, they become impossible to accelerate because they begin gaining mass from the very energy that is pushing them! This is embodied in the famous equation, E = mc2, which states that energy can be converted into mass and vice versa. Approximately speaking, particles near lightspeed gain mass rather than energy, or to put it another way, they get heavier but they don't go faster when you add energy to them. (One cannot help but think of a fat pig, stuffing down lots of food energy but getting fatter and slower rather than faster and more powerful.) Using this fact, Chandrasekhar noted that the electron pressure in a white dwarf must have an absolute limit. Even if crushed to infinite density, the speed limit imposed by relativity would still force a cut-off to any pressure they could exert.

Subrahmanyan Chandrasekhar
At the same time, alarmingly, there is no limit to how much mass you can pile onto a white dwarf. Worse, the heavier you make one the more powerful the gravitational force at its surface becomes. Isaac Newton's famous Law of Universal Gravitation states that the force of gravity is proportional to 1/r2, which means that if a planet's radius shrinks by a factor of two, then the force of gravity at its surface must rise by a factor of four.
Chandrasekhar showed that there was a point where the unlimited advance of increasing mass and decreasing radius could no longer be sustained. Like a straw breaking a camel's back, adding more mass to a white dwarf at this point would cause the dwarf's gravitational compression to exceed any possible increase in electron pressure. Thus the dwarf would shrink, yet be left with an even worse gravitational imbalance than before. The increased imbalance would make it shrink further, thus worsening the gravitational crisis . . .
In short, Chandrasekhar's calculations predicted that if a white dwarf was raised beyond a critical mass, it would catastrophically collapse! He calculated this critical mass to be about 1.4 times the mass of the Sun, and in time it came to be known as Chandrasekhar's Limit.
It would be fair to say that this news got a highly mixed reception in 1931. Quantum mechanics was still a very young subject at that time (only four years old) and many astrophysicists still had grave doubts about the entire theory of quantum mechanics, never mind the believability of this particular prediction. How, they scoffed, could an object half again as massive as the Sun and already compressed to an almost unimaginable density, just "collapse"? Collapse to what? It was utterly preposterous. If taken to its logical conclusion, Chandrasekhar's work indicated that a white dwarf pushed above the limit would literally disappear – or more exactly, it would be instantly compressed to an infinitesimal point. There was no lack of astronomers who were skeptical about this idea, to put it mildly. Sir Arthur Eddington, the first astronomer to verify Einstein's prediction that the Sun's gravity could bend starlight, and possibly the most respected astronomer of his time, simply dismissed the prediction out of hand. Indeed, it was largely Eddington's vocal criticism of the theory that caused it to be almost disregarded for the better part of a decade.

Arthur Eddington
And yet, by this time astronomers had discovered dozens of white dwarf stars . . . and not one had a mass above 1.4 solar masses, as far as could be determined. There were a few who felt that this was too eerily in accord with Chandrasekhar's Limit for the whole idea to just be dismissed. As we shall see later, the full story of what happens when a white dwarf is taken beyond 1.4 solar masses turns out to be wonderful and complicated, but before we can tell that story we must turn our attention to stellar birth, which we will do in the next section.
Before moving on, I will note that in 1937, weary of the hostility to his theories from Eddington and other British astronomers, Chandrasekhar left Cambridge for a faculty position at the University of Chicago, where he stayed for the rest of his life. In 1983 he was awarded the Nobel Prize in Physics, primarily for his work on white dwarfs.
For a translation of this page into other languages, click a link below.
Bosnian, Croatian, Estonian, Georgian, Hindi, Norwegian, Polish, Russian, Spanish, Turkish, Ukrainian