1814 - Joseph Fraunhofer, a German lens-maker and optical scientist, has become the world's finest craftsman in optical glass. He is testing a new and especially fine prism by shining sunlight through it when he notices, to his astonishment, that the spectrum of the sun (the rainbow produced when white light is passed through a prism) is not continuous! It is divided by dozens of fine black lines. No one before Fraunhofer has seen the lines because their prisms were not large enough nor well enough made. The presence of the lines is a complete mystery to physicists, and will remain so for 45 years.

Solar spectrum, showing dark absorption lines

Line spectrum from incandescent gas
Over that same 45 years, various chemists notice that elements which have been vaporized into incandescent gas give off spectra which consist of discrete bright lines rather than a continuous rainbow. No one connects this fact with the solar mystery until 1859.
1858 - Julius Plucker, a German physicist, tries an experiment in which he embeds metal plates into either end of an evacuated glass tube and then places a high voltage across the plates. (Plucker thought that maybe electricity was a fluid of some kind, and the general idea of his experiment was to see if he could force the "electric fluid" to squirt out where he could see it.) Well, he doesn't see any electric fluid, but he does notice that the tube glows an eerie green, and that the pattern of the green light can be shifted with a magnet.
Tech Note - All Plucker was doing was sending electrons through the space between the two metal plates. An electric current is just electrons, and if you send a current across a vacuum, then the electrons become freely moving particles. The green light Plucker saw was free electrons whacking into the atoms in the glass and exciting their spectral lines (like the lines shown above), some of which happened to be green. Spectral lines are created whenever the bound electrons in an atom are jumping from one energy level to another, and this jumping can be caused by heat, by particle impact, by incoming electromagnetic radiation, etc. The pattern could be shifted with a magnet because moving electrons (like all moving charged objects) are affected by magnetic fields.
1859 - Gustav Kirchhoff, a German physicist, is studying the bright spectral lines given off when elements are heated to incandescence. By this time it is well-known that light is a wave, and that different colors correspond to different frequencies. Kirchhoff realizes that every element produces an unique set of lines, a spectral "fingerprint", so to speak - which means that every element is associated with a unique set of frequencies. Using statistical physics and conservation of energy arguments, he deduces that dark lines in the solar spectrum and bright lines in heated laboratory gases are part and parcel of same thing. The laboratory spectra (bright lines against a dark background) are created as the hot elements emit light at specific frequencies. The solar spectrum (dark lines against a rainbow background) is created by gaseous elements in the solar atmosphere as they absorb those exact same frequencies from the light shining through them. Kirchhoff does not know, however, how the spectral lines are produced in the first place.
Tech Note - Kirchhoff could not know it, but this is just the way quantum mechanics works. It limits the atom to emitting energy (light) at only specific wavelengths, and also limits it to only absorbing energy at those same wavelengths. More details are given in the entries for 1913 to 1927.
1860 - As a method of studying light emission without the complications of spectral lines, Kirchhoff suggests that researchers use a closed chamber which has been heated red-hot, then peek into the chamber through a very small hole. Since the atoms in the closed chamber must both emit and absorb their own spectral lines, the overall spectrum will be continuous. (That is, the spectral lines emitted by any type of atom will be resonantly absorbed by other atoms of the same type, canceling each other out. There will be no dark or bright lines.) The interior of such a chamber comes to be known as a "black body". It is thought to be the perfect example of a simple system in which heat is transformed into electromagnetic waves (light) by classic physics.
1876 - Eugen Goldstein, a German physicist, is studying the flow of electric current through a vacuum, using the same technique as Plucker (see 1858). By putting barriers in the tube, he notices that the fluorescence of the glass seems to be caused by a beam of some sort flowing from the negative plate (which is called the cathode) to the glass. He calls the beam a "cathode ray". Electrons will thus be called "cathode rays" for the next 30 years.
1880 - William Crookes, an English physicist, creates a greatly improved version of the vacuum tube (the "Crookes tube") and proceeds to show that cathode rays travel in straight lines, cast sharp shadows, and carry an electrostatic charge. He even puts a little paddle wheel into one tube and shows that the cathode rays can turn the wheel when they hit it, just like a stream of water! He concludes that cathode rays are actually a stream of charged particles.
1887 - Heinrich Hertz, who will discover radio waves in the next year, notices that certain spark coils he uses work more easily if ultraviolet light is shining on them. He does not know it, but this is the first observation of the photoelectric effect.
Tech Note - The photoelectric effect occurs because under certain circumstances light can eject electrons out of a metal. Spark coils work more-or-less like electrostatic machines: they build up a voltage until the electric potential is high enough to allow the electrons to rip through the air between the electrodes, thus creating a bright spark. By shining an ultraviolet light on the spark coil, Hertz was releasing electrons via the photoelectric effect and thus making it easier for a spark to develop.
1885 - Johann Balmer, a Swiss high-school teacher, notices that the exact frequencies of the spectral lines seen in incandescent hydrogen can be predicted by the formula:
(Balmer Formula)
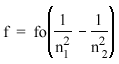 , where n1 and n2 are integers (n2 > n1) and fo = 3.29 X 1015 Hz. , where n1 and n2 are integers (n2 > n1) and fo = 3.29 X 1015 Hz. |
| Balmer has discovered his formula through sheer persistence. He has spent years studying the frequencies of the hydrogen lines, and he eventually uncovers this. He does not know why the formula works, but he finds it interesting and publishes it in a scientific journal. |
 1890 - Entry from the Encyclopedia Britannica: "The spectrum of a body is due to periodic motion within the molecules. It seems probable that there is a numerical relation between the different periods of the same vibrating system. In organ pipes or stretched strings the relation is a simple one, these periods being a submultiple of the fundamental period. The harmony of a compound sound depends on the fact that the different times of vibration are in the ratio of small integer numbers. We may with advantage extend the expression harmonic relation to light."
1890 - Entry from the Encyclopedia Britannica: "The spectrum of a body is due to periodic motion within the molecules. It seems probable that there is a numerical relation between the different periods of the same vibrating system. In organ pipes or stretched strings the relation is a simple one, these periods being a submultiple of the fundamental period. The harmony of a compound sound depends on the fact that the different times of vibration are in the ratio of small integer numbers. We may with advantage extend the expression harmonic relation to light."
This entry demonstrates that spectral lines were still considered, in 1890, to be a complicated but entirely classical problem - the optical analog to the finding resonant sound frequencies in a Scottish bagpipe.
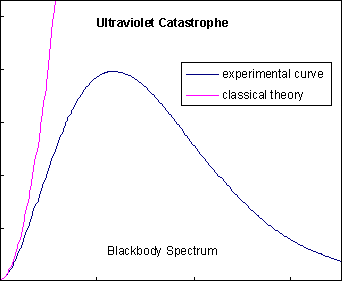
By 1890, many experimental physicists had turned their attention to studying blackbody radiation, as suggested by Kirchhoff, to avoid dealing with spectral lines. They had discovered that a graph of the intensity of the radiation versus its frequency made a certain type of bell curve, which had come to be called the "blackbody spectrum". The problem was, classic electrodynamics and statistical physics predicted that the blackbody spectrum would race off to infinity as the frequency increased, not roll over in a bell curve as shown at left. This became known as the "ultraviolet catastrophe", because it was obviously impossible for the energy radiated by a blackbody to be infinite, and because ultraviolet frequencies were about where classical theory and experimental data parted ways. The search for an explanation of the blackbody spectrum is considered to be one of the most important problems in theoretical physics at this time.
1895 - William Roentgen, a German physicist, discovers that Crookes tubes also emit invisible rays which travel outside the tube and can fog photographic plates even when paper, wood, and similar materials are positioned between the plate and the tube. The rays are unaffected by magnets, so they cannot be cathode rays (electrons). Roentgen doesn't know what the rays are, so he calls them "X-rays" (after X, the traditional unknown quantity in mathematics). The idea that X-rays are electromagnetic radiation of very short wavelength is soon being discussed by physicists, but this will not be proven until 1912.
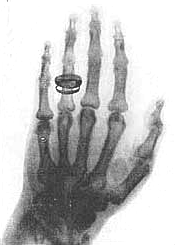 One of Roentgen's first X-ray photographs is a picture of the bones in his wife's hand (actual photo shown at left). It creates a world-wide sensation and 1000 scientific papers about X-rays are published within the next year. Within three years X-rays are being used by the medical profession for diagnosis.
One of Roentgen's first X-ray photographs is a picture of the bones in his wife's hand (actual photo shown at left). It creates a world-wide sensation and 1000 scientific papers about X-rays are published within the next year. Within three years X-rays are being used by the medical profession for diagnosis.
Tech Note - Exactly as discussed under the Plucker entry for 1859, the X-rays in the Crookes tube were being created by electrons whacking into the glass and exciting it to emit spectral lines. The only difference is, the X-rays emitted by the Crookes tubes have much higher energies and therefore much shorter wavelengths than do spectral lines of visible light.
1897 - J. J. Thomson, an English physicist, conducts a series of experiments on "cathode rays" and demonstrates that they consist of a stream of small, electrically charged particles which have a mass over a thousand times less than that of a hydrogen atom. Thomson has discovered the electron. From this point onward, it becomes increasingly clear that atoms are not fundamental particles, but in fact are made up of smaller particles.
1900 - In the first year of the new century, German physicist Max Planck presents a paper to the German Physical Society in which he derives the (experimental) blackbody formula. Planck has used the old trick of taking the known experimental results and working backwards to see what he has to do to make it square with known theory. In this case, Planck has found that he can only make things work out if he uses a peculiar assumption: he has not allowed the atoms to share energy continuously, but instead has assumed that they can only transfer energy from one to another in discrete bundles, or quanta. The formula which determines the energy transfer is:
 E = nhf
E = nhfwhere n is an integer from one to infinity, f is the frequency of the electromagnetic radiation, and h is a constant. By comparing his formula to the experimental data on blackbody radiation, Planck determines that the value of the constant is: h = 6.63 X 10-34 joule-second. It is soon realized that Planck's constant is a fundamental constant of nature, equally as important as the speed of light or the charge on an electron.
Planck does not believe that his formula represents a radical departure from classical physics, however. He believes (as do all the physicists who listen to his talk) that this quantization of the blackbody formula represents yet another complex resonance effect of some sort, like those thought to be responsible for atomic spectra.
1902 - Philipp Lenard, a French physicist, investigates the photoelectric effect. He discovers that the photoemission of electrons from a metal has a strange property: the frequency of the light, not its intensity, determines whether there is emission. That is, if the frequency is above a certain threshold, then electrons are immediately emitted, no matter how weak the light is. Conversely, if the frequency is below the threshold, then no electrons are emitted, regardless of how strong the light is.
This result cannot be explained by Newtonian physics, because the energy carried by a classic wave is dependent on the intensity, not the frequency. Bright light of any frequency should be able to drive off electrons, in a Newtonian picture. Similarly, if the light is very dim, then Newtonian physics says that there must be a considerable time delay as the electrons slowly absorb the necessary energy. They should not come flying off instantly. Lenard's results - which are exactly the opposite of this - are equivalent to saying that electrons are like very odd beach pebbles which are immovable if hit by a low-frequency tidal wave, but will instantly rocket clear off the beach if touched by a high-frequency splash from a petulant mosquito.
1905 - Albert Einstein, a clerk in the Swiss Patent Office and sometime physicist, publishes a paper in which he outlines a possible explanation for the photoelectric effect. Suppose that light does not carry energy in a continuous fashion, as would be expected for a classical wave, but instead carries it in bundles, which come later to be called photons. (Einstein did not invent that term.) Suppose further that the energies of these photons are given by the Planck formula, E = hf. Then one can see why the photoelectric effect depends on the frequency of the light: the electrons will not be detached from the material unless they receive a large enough "bundle" of energy, and since the size of the "bundle" depends on the frequency, only light above a certain frequency will generate the photoelectric effect.
By no means was Einstein saying that light is a particle. He was only saying that the energy in the wave, for some reason, can only be delivered in bundles rather than continuously. He predicts that measurements of the energy of the electrons emitted by the photoelectric effect will be given by the equation E = hf - 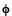 , where
, where 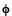 is the amount of energy needed to initially remove the electron from the metal. Since the constant "h" is already known from blackbody measurements (a seemingly much different phenomena), this is a strong prediction. For technical reasons, due to the considerable difficulty of generating variable-frequency ultraviolet light and of accurately measuring electron energies in a vacuum, this prediction cannot be verified for some years.
is the amount of energy needed to initially remove the electron from the metal. Since the constant "h" is already known from blackbody measurements (a seemingly much different phenomena), this is a strong prediction. For technical reasons, due to the considerable difficulty of generating variable-frequency ultraviolet light and of accurately measuring electron energies in a vacuum, this prediction cannot be verified for some years.
1909 - Eugene Marsden and Hans Geiger (who will later invent the Geiger counter) are two graduate students working with nuclear physicist Ernest Rutherford in Manchester, England. They perform a series of experiments in which gold foil is bombarded by heavy, fast-moving subatomic particles known as "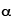 -particles". (See the Particle & Nuclear Timeline for more details about
-particles". (See the Particle & Nuclear Timeline for more details about 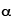 -particles.) Matter at this time is generally thought to be smooth, even if it does consist of atoms. A popular model is J. J. Thompson's "plum pudding" model, in which positively-charged matter is thought of like a pudding, and electrons are thought to be embedded in the goo like raisins. Rutherford is investigating what happens when bullets are fired into the pudding.
-particles.) Matter at this time is generally thought to be smooth, even if it does consist of atoms. A popular model is J. J. Thompson's "plum pudding" model, in which positively-charged matter is thought of like a pudding, and electrons are thought to be embedded in the goo like raisins. Rutherford is investigating what happens when bullets are fired into the pudding.
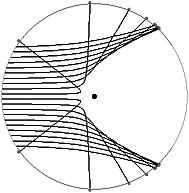 |
|
|
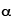 -particles go through the gold with little or no deflection, as expected - but a few are deflected through large angles, and a very few even turn around and bounce straight back as though they have hit an impenetrable barrier! (Rutherford says later that this is the most astounding thing ever to happen to him. In a speech he says it was liking firing a cannon at a piece of soggy tissue paper, and watching the cannonball ricochet off.) Rutherford proposes the "solar system" model of the atom, in which the atom is basically empty space but has a very small and incredibly dense nucleus. This is the only reasonable explanation of the experimental results. Later, theoretical analysis shows that the observed angular spread of the particle scattering is exactly what would be predicted by a random spray of particles passing a heavy center, and being deflected by the Coulomb force (see figure). This provides virtually irrefutable proof that the solar system model must be correct.
-particles go through the gold with little or no deflection, as expected - but a few are deflected through large angles, and a very few even turn around and bounce straight back as though they have hit an impenetrable barrier! (Rutherford says later that this is the most astounding thing ever to happen to him. In a speech he says it was liking firing a cannon at a piece of soggy tissue paper, and watching the cannonball ricochet off.) Rutherford proposes the "solar system" model of the atom, in which the atom is basically empty space but has a very small and incredibly dense nucleus. This is the only reasonable explanation of the experimental results. Later, theoretical analysis shows that the observed angular spread of the particle scattering is exactly what would be predicted by a random spray of particles passing a heavy center, and being deflected by the Coulomb force (see figure). This provides virtually irrefutable proof that the solar system model must be correct.
Several physicists immediately point out a serious problem with this model: an orbiting electron must be accelerating, and an accelerated charge must radiate electromagnetic energy, according to Maxwell's equations. Therefore, the electron should quickly lose all its kinetic energy and spiral into the nucleus, causing the atom (and thus all matter) to collapse.
1911 - Robert Millikan, a physicist at the University of Chicago, measures the charge on the electron to within 1%. He does this by spraying very fine oil droplets into a chamber with a perfume atomizer, then watching the droplets with a tele-microscope to see if any of them have happened to pick up a static electric charge from the friction of being sprayed in. Millikan could tell if the droplets were charged or not because he'd set up things such that he could put an electric field (i.e., a voltage differential) across the chamber. The uncharged droplets would fall to the bottom, but the charged droplets would be attracted by the electric field and float. Millikan could measure the charge on the oil droplet by carefully adjusting the voltage to exactly balance the force of gravity, thus making the droplet float in one spot. Millikan works on this experiment for eleven years(!) and eventually has enough data to prove that the charge on the electron is fixed at 1.6 X 10-19 coulomb. He also shows that he has never seen a charge of any size which would involve a fraction of an electron's charge; he has only seen charges that are even multiples of the electron's charge. He thus provides strong evidence that the charge on the electron is the smallest, most fundamental unit of charge in the Universe.
This near-legendary experiment is considered to be one of the most laborious ever carried out by one man. The University of Chicago has preserved the chamber where Millikan sat staring through his tele-microscope, year after year, waiting patiently for stray electrons to float into view so that he could painstakingly balance them by hand with a variable voltage source. Millikan won the 1923 Nobel Prize, mostly for this work.
1913 - The Danish physicist Neils Bohr has been working on the most critical problem with Rutherford's "solar system" atom, which is that a rotating electric charge should quickly radiate away all its energy (see 1909). As a way out of this, he hypothesizes that an orbiting electron can only radiate or absorb energy in quantized packets, similar to the ideas proposed by Einstein for the photoelectric effect and by Planck for the black-body formula. This would automatically stabilize the atom against the energy-radiation problem, and even better, finally provide a good reason for why atoms exhibit spectral lines when they are excited.
 If an electron can only be in certain energy levels, then it can only give up or absorb energy by moving between those levels. The energy differences between these levels must correspond to specific frequencies (using E = hf), thus only those frequencies (colors) of light can be emitted. In the figure at left, we are shown six quantized energy levels in a hypothetical atom. There are four arrows, representing quantum transmissions (electron jumps) from levels 6, 5, 4, and 3 down to level 2. When the electron jumps from a higher energy level to a lower energy level, then it loses energy and that has to go somewhere. Where it goes is into a single photon whose energy exactly equals the energy left over after the electron has jumped to a lower level. In the spectrum at the top, we are shown that the violet line corresponds to the photons emitted as electrons jump from level 6 to level 2. Likewise, the bluish line represents the transition from level 5 to level 2, and so forth.
If an electron can only be in certain energy levels, then it can only give up or absorb energy by moving between those levels. The energy differences between these levels must correspond to specific frequencies (using E = hf), thus only those frequencies (colors) of light can be emitted. In the figure at left, we are shown six quantized energy levels in a hypothetical atom. There are four arrows, representing quantum transmissions (electron jumps) from levels 6, 5, 4, and 3 down to level 2. When the electron jumps from a higher energy level to a lower energy level, then it loses energy and that has to go somewhere. Where it goes is into a single photon whose energy exactly equals the energy left over after the electron has jumped to a lower level. In the spectrum at the top, we are shown that the violet line corresponds to the photons emitted as electrons jump from level 6 to level 2. Likewise, the bluish line represents the transition from level 5 to level 2, and so forth.
Note that the transition 3 to 2 gives a red line (longer wavelength, lower frequency, lower-energy photons), whereas the transition 6 to 2 gives a violet line (shorter wavelength, higher frequency, more energetic photons). This is the way it must be, because level 6 is above level 3 in energy, so when the electron drops to level 2 it must give up more energy in the 6 to 2 transition than in the 3 to 2. So the photons given off by the 6 to 2 transition are violet (higher energy), and the 3 to 2 photons are red (lower energy).
The diagram only shows transitions down to level 2, but any combination is possible: 4 to 1, 5 to 4, 6 to 3, 2 to 1, anything you like. It is also possible to turn things around and have the electron jump up to higher levels: 2 to 6, 1 to 2, 3 to 5, whatever. The only difference is, to jump up the electron must gain energy from an incoming photon. Quantum mechanics plus the conservation of energy demand that if the electron is to make, for example, the 2 to 4 transition, then it must acquire exactly the amount of energy separating level 2 and level 4. Not less, not more, exactly. From the diagram you can see that the atom emitted a greenish photon when electrons made the 4 down to 2 jump. Since the energy between the levels is exactly the same whether you're going up or down, that means the only photons capable of exciting the 2 to 4 upward transition are those with exactly the same color (frequency) as the greenish 4 to 2 line in the spectrum.
 |
|
|
where m = mass of the electron, k = the electrostatic force constant, e = the charge on the electron, and h = Planck's constant. When one puts in the values for all these constants, one does indeed get fo. It was clear that there had to be something "real" in this idea, but Bohr was unable to explain finer details of the hydrogen spectrum, or to extend the theory to other atoms.
1915 - The German physicist Arnold Sommerfeld extends Bohr's ideas about the hydrogen atom by including elliptical orbits as well as circular ones. He also incorporates relativity into the model. In this way he is able to explain considerably more details in the hydrogen spectrum than Bohr did - but the theory still cannot be extended to other atoms.
1915 - Robert Millikan, after nearly ten years of work on improved vacuum chambers, has finally completed his research on Einstein's prediction for the photoelectric effect (see 1905) -- which, by the way, Millikan is completely certain is total nonsense. (Legend has it that when one of Millikan's assistants took some preliminary data that seemed to verify Einstein's equation, Millikan decided to do all of the rest of the work personally, to be certain it was correct.) But after two years of experiments, Millikan is reluctantly forced to admit that E = hf. In announcing his results, Millikan writes, "Einstein's photoelectric equation appears in every case to predict exactly the observed results. Yet the physical theory of which it was designed to be the symbolic expression is found so untenable that Einstein himself, I believe, no longer holds it."
Ha. Einstein was actually moving ahead with the quantum idea, and by 1916 had concluded that his "photons" not only carried discrete amounts of energy, but also carried momentum, given by the formula p = hf / c. Millikan is rather famous (or infamous) as the classic example of how many of the older physicists of this period simply never believed in quantum mechanics. Millikan lived until 1953, when he was 85, and even as late as 1948 he was still saying "I spent ten years of my life testing that 1905 equation of Einstein's, and contrary to all my expectations, I was compelled in 1915 to assert its unambiguous verification in spite of its unreasonableness, since it seems to violate everything we know about the interference of light."
Not that Millikan didn't admit that there had to be something to this Einstein-Bohr-Planck quantum stuff. It worked too well to be completely wrong. But he, and many other physicists of his generation, always believed that quantum mechanics was fundamentally wrong, somehow. The gap between quantum uncertainty and Newtonian mechanics was just too much for them to accept. Towards the end of his life, Max Planck commented that the new ideas in physics had gradually taken over only because everyone who believed in the old ones had died. If there is an epitome for this remark, Millikan is it.
1916 - American chemist Gilbert Lewis proposes (correctly) that the arrangement of electrons into quantum "shells" around atoms is the basic mechanism responsible for chemistry.
1923 - French physicist Louis de Broglie presents theoretical arguments which indicate that everything should obey the Einstein formula for the momentum of a photon. Using the fact that c = f  , we have: p = hf / c = h /
, we have: p = hf / c = h /  , where h is Planck's constant and
, where h is Planck's constant and  is the wavelength of either a photon or a particle. In other words, not only should light behave like a particle, in certain ways, but particles should also behave like waves, in certain ways. Planck's constant is so small, however, that even a wavelength of a nanometer is only going to have a momentum of 6.6 X 10-34 J-sec / 10-9 m = 6.6 X 10-25 kg m/s2. Which is a very small amount of momentum. This means that only very small particles will show the wave phenomena to any appreciable degree, and de Broglie realizes that only electrons are likely to show wave-particle duality clearly enough to be observed. He predicts that electrons can be diffracted like X-rays, with their wavelength and momentum connected by:
is the wavelength of either a photon or a particle. In other words, not only should light behave like a particle, in certain ways, but particles should also behave like waves, in certain ways. Planck's constant is so small, however, that even a wavelength of a nanometer is only going to have a momentum of 6.6 X 10-34 J-sec / 10-9 m = 6.6 X 10-25 kg m/s2. Which is a very small amount of momentum. This means that only very small particles will show the wave phenomena to any appreciable degree, and de Broglie realizes that only electrons are likely to show wave-particle duality clearly enough to be observed. He predicts that electrons can be diffracted like X-rays, with their wavelength and momentum connected by:
(de Broglie wavelength equation) p = h /
1925 - German physicist Werner Heisenberg (who is only 24 years old) concludes that the astronomical-oriented ideas of Bohr and Sommerfeld and others - who describe spectral lines in terms of electrons in elliptical orbits, tilted orbits, rotation around an axis, and so forth - are totally useless. He develops matrix mechanics, in which pure numbers representing the energy and momentum of electron orbitals are manipulated without any regard for what they might mean in terms of a physical picture. This is the beginning of modern quantum mechanics.
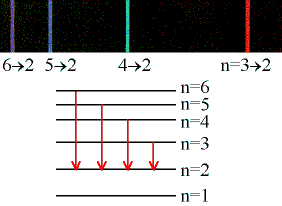
1926 - Almost simultaneously with Heisenberg, Austrian physicist Erwin Schrodinger develops a theory of electron motion which also discards the astronomical-orbits ideas of Bohr and Sommerfeld. His theory, however, becomes known as wave mechanics because in this theory the electron is visualized as a wave-type entity which is literally everywhere at once, and only "collapses" to a point when it interacts with other matter. Schrodinger works out possibly the most useful equation in modern physics, the Schrodinger wave equation, which says that the absolute position of matter is almost a meaningless question. All that one can do is calculate a relative probability that it might be somewhere as compared to somewhere else. Schrodinger's equation is actually a general formulation that must be tailored to each specific problem, so its exact form varies depending on the circumstances. A particularly simple version is the one for the hydrogen atom:
(Schrodinger wave equation for the hydrogen atom)
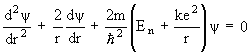
where 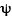 is the probability wave of the electron, r is the electron's distance (radius) from the center of the atom, m is the mass of the electron, h-bar is Planck's constant divided by 2
is the probability wave of the electron, r is the electron's distance (radius) from the center of the atom, m is the mass of the electron, h-bar is Planck's constant divided by 2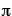 , E is the energy of the electron, k is the electrostatic constant, and e is the charge on the electron. Within months Heisenberg demonstrates that his theory and Schrodinger's are, in fact, exactly equivalent mathematically. That is, they are really saying the same thing, but using much different representations.
, E is the energy of the electron, k is the electrostatic constant, and e is the charge on the electron. Within months Heisenberg demonstrates that his theory and Schrodinger's are, in fact, exactly equivalent mathematically. That is, they are really saying the same thing, but using much different representations.
Education Note - The Schrodinger wave equation is considerably easier to visualize and to work with than Heisenberg matrix mechanics, so the Schrodinger version of quantum mechanics is almost exclusively what is discussed in popular science books and in introductory physics textbooks.
1927 - Heisenberg enunciates his now-famous Uncertainty Principle. In brief, the principle states that it is impossible to know both the position and momentum of a particle with infinite precision. This is not a statement about the accuracy of any instrument. Even if you have a perfect instrument capable of making perfect measurements, the Uncertainty Principle still holds because it is concerned with the fundamental nature of quantum mechanics. Uncertainty is a basic part of physics, at the quantum level.
Mathematically, the principle can be stated as:
(for momentum)
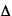 p
p 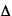 x > h / 2
x > h / 2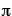
(for energy)
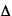 E
E 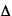 t > h / 2
t > h / 2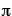
where 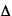 p,
p, 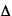 x,
x, 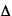 E and
E and  t represent the (separate) uncertainties in momentum, position, energy, and time, respectively, and h is Planck's constant.
t represent the (separate) uncertainties in momentum, position, energy, and time, respectively, and h is Planck's constant.
1927 - In the United States, physicists Clinton Davisson and John Germer are experimenting with electron beams. They are trying to use the electrons as a probe to study the oxidation of nickel (a problem of modest practical importance to the electroplating industry). Electron beams can only be generated in a vacuum, and in 1927 the only practical way to make a decent vacuum chamber is to blow it out of glass, so Davisson and Germer hire a glass-blower to blow a complete bubble around each nickel sample. To get at the sample, they have to break the glass.
The only way they can clean their samples once the samples are inside the glass is to heat them white-hot, just like you can heat a light-bulb filament, by running electricity through them. So, they are doing this one day when somebody accidentally drops a wrench on the glass and breaks it and poof! Their nice ultra-pure, white-hot nickel sample instantly reacts with the air and becomes very heavily oxidized.
Davisson and Germer have another bubble blown, and are soon heating their nickel sample again. It is now so heavily oxidized, however, that they have difficulty in getting it down to bare metal. So, they heat it hotter and hotter in an effort to clean it, and accidentally melt it. Fortunately, the drop of liquid metal doesn't fall off the sample holder, so they just calmly allow it to cool down again so that they can work with the resolidified nickel. (It is terribly time-consuming to break the glass and reblow another bubble.)
 |
|
|
Tech note - Slowly cooling molten metals is a "standard" way to produce metal crystals, if one wants a metal crystal. If the metal is cooled quickly (as is usually the case) then the atoms don't have time to form a single large crystal, so you end up with a polycrystal, so-called because it consists of many, many tiny crystals of metal all jumbled together. The metal you have contact with in everyday life is overwhelmingly polycrystalline. Davisson and Germer's expertise in metallurgy allowed them to immediately realize that they had accidentally produced a single crystal of nickel in their glass bubble.
Davisson and Germer are old-fashioned "practical" physicists who rarely read theoretical journals (especially those written in some foreign language - like German), who don't think much about philosophical implications, and who spend most of their time tinkering in the laboratory. They have never heard of de Broglie, Heisenberg, or Schrodinger, never mind being familiar with their theories. Davisson and Germer are convinced they have evidence that the electrons are being channeled between the rows of nickel atoms in the single crystal. They prepare a paper of no scientific value whatever which announces this "discovery".
But, fate intervenes. Davisson is a mountaineering enthusiast of the highest sort (He will die at the age of 77 when he falls during a mountain-climbing expedition.) and he takes a vacation in the Swiss Alps just after the paper is written, but before it has been published. He discusses his work with European colleagues who immediately recognize that what he and Germer are seeing is nothing less than electron diffraction - direct proof of wave mechanics! A precise comparison of the directions where Davisson and Germer have measured electron beams coming off the nickel and the positions predicted by wave mechanics leaves no doubt: the electrons are diffracting off the individual nickel atoms and interfering with each other as they leave the surface, thus producing an interference pattern which manifests itself as multiple reflected beams.
Davisson and Germer rewrite their paper to include the effects of quantum mechanics. The final version is 30 pages long - and only the first five discuss the sensational discovery of electron diffraction. The other 25 pages are a rather boring exposition of the patterns which form on the surface of single-crystal nickel when it is lightly oxidized.
Post 1927 - Over the next several decades, Schrodinger's wave mechanics is extended and applied by many physicists to a wide variety of problems. A picture gradually emerges in which quantum mechanical particles (such as the photon or the electron) come to be seen as entities unto themselves - neither particles nor waves, nor even some sort of hybrid particle/wave "duality". They are recognized as fundamental particles which simply obey different rules than those that apply to the macroscopic world.


Perhaps the most startling difference between the behavior of an electron and a classical particle is that the electron does not exist at a single point. Rather, depending on its energy, angular momentum, magnetic state, and other factors, it becomes a "probability cloud" in which only your relative chances of interacting with the electron at a point can be known. The figure at above left shows computer-generated plots of the probability clouds for various energy and momentum states in the hydrogen atom. The figure at above right shows the electron probability distribution around a water molecule. In the water molecule, the cloud is made up of multiple electrons, all with overlapping probabilities. (The grainy quality in the water molecule drawing is only an artist's rendition. Electrons are not little grains that hop around inside their probability clouds; they are the probability cloud.)
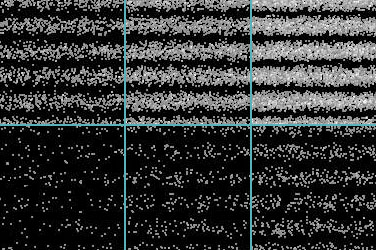 As technology improves, it becomes possible to carry out a fairly dramatic demonstration of the reality of Einstein's photons. The usual double-slit arrangement for producing wave interference is set up, and a phosphorescent screen is put into place to detect the light. However, in this experiment the light source used is so weak that its energy is equivalent to only one photon at a time passing through the slits. The result is shown in the figure at right. The individual photons "ping" on the screen as distinct flashes, leaving a dot. At first the dots appear to be randomly scattered, but as time goes on a clear pattern emerges: the dots are hitting the screen with a probability pattern exactly equal to what it would be if they were classic waves.
As technology improves, it becomes possible to carry out a fairly dramatic demonstration of the reality of Einstein's photons. The usual double-slit arrangement for producing wave interference is set up, and a phosphorescent screen is put into place to detect the light. However, in this experiment the light source used is so weak that its energy is equivalent to only one photon at a time passing through the slits. The result is shown in the figure at right. The individual photons "ping" on the screen as distinct flashes, leaving a dot. At first the dots appear to be randomly scattered, but as time goes on a clear pattern emerges: the dots are hitting the screen with a probability pattern exactly equal to what it would be if they were classic waves.
Even more remarkably, when this experiment is repeated some years later with electrons, exactly the same thing happens. The electrons are sent one at a time through the slits, and "ping" against the screen as though they are particles - but the pattern of their distribution across the screen is that of an interference wave. There is no longer any question that the classical notions of "waves" and "particles" only make sense in the macroscopic world. At the microscopic level, there is only quantum mechanics.
 Relativity
|
Nuclear & Particle Physics
Relativity
|
Nuclear & Particle Physics 
For a Ukrainian translation of this page, see Nocramming.com
